题目内容
9．
如图所示，将截面为正方形的真空腔abcd放置在一匀强磁场中，磁场方向垂直纸面向里．若有一束具有不同速率的电子由小孔a沿ab方向射入磁场，打在腔壁上被吸收，则由小孔c和d射出的电子的速率之比2：1；通过磁场的时间之比为1：2．
分析 电子垂直射入匀强磁场中，由洛伦兹力提供向心力，做匀速圆周运动．根据牛顿第二定律推导出电子圆周运动的速率与半径的关系．根据几何知识确定电子从c孔和b孔时半径关系，求解速率之比．根据时间与周期的关系，求解时间之比．
解答 解：①设电子的质量为m，电量为q，磁感应强度为B，电子圆周运动的半径为r，速率为v，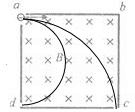
由牛顿第二定律得：evB=m$\frac{{v}^{2}}{r}$，
解得：v=$\frac{eBr}{m}$，r与v成正比．
由图看出，从c孔和d孔射出的电子半径之比rc：rd=2：1，则速率之比vc：vd=rc：rd=2：1．
②电子圆周运动的周期为：T=$\frac{2πm}{eB}$，所有电子的周期相等，
从c孔和d孔射出的电子在盒内运动时间分别为：tc=$\frac{1}{4}$T，td=$\frac{1}{2}$，
所以从c孔和d孔射出的电子在盒内运动时间之比：tc：td=1：2；
故答案为：2：1，1：2．
点评 本题属于带电粒子在磁场中的偏转中典型题目，此类题的关键在于确定圆心及由几何关系求出半径．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
电动机牵引一根原来静止的、长L=1m、质量m=0.1kg的导体棒R=1Ω，竖直轨道处于B=1T的磁场中，当棒由静止上升h=3.8m时获得稳定的速度，该过程回路共产生14J的热量．电压表和电流表的示数分别为7V和1A．电动机内阻为1Ω，g=10m/s2．求：
如图，一固定的竖直气缸有一大一小两个同轴圆筒组成，两圆筒中各有一个活塞，已知大活塞的质量为m1=2.50kg，横截面积为s1=80.0cm2，小活塞的质量为m2=1.50kg，横截面积为s2=40.0cm2；两活塞用刚性轻杆连接，间距保持为l=40.0cm，气缸外大气压强为p=1.00×105Pa，温度为T=303K．初始时大活塞与大圆筒底部相距$\frac{l}{2}$，两活塞间封闭气体的温度为T1=495K，现气缸内气体温度缓慢下降，活塞缓慢下移，忽略两活塞与气缸壁之间的摩擦，重力加速度g取10m/s2．求：
质谱仪原理如图所示，a为粒子加速器，电压为U1；b为速度选择器，磁场与电场正交，磁感应强度为B1，板间距离为d；c为偏转分离器，磁感应强度为B2．今有一质量为m、电荷量为e的正电子（不计重力），经加速后，该粒子恰能竖直通过速度选择器，粒子进入分离器后做半径为R的匀速圆周运动．则：
驾驶证考试中的路考，在即将结束时要进行目标停车，考官会在离停车点不远的地方发出指令，要求将车停在指定的标志杆附近，终点附近的道路是平直的，依次有编号为A、B、C、D、E的五根标志杆，相邻杆之间的距离△L=12.0m．一次路考中，学员甲驾驶汽车，学员乙坐在后排观察并记录时间，学员乙与车前端面的距离为△s=2.0m．假设在考官发出目标停车的指令前，汽车是匀速运动的，当学员乙经过O点考官发出指令：“在D标志杆目标停车”，发出指令后，学员乙立即开始计时，学员甲需要经历△t=0.5s的反应时间才开始刹车，开始刹车后汽车做匀减速直线运动，直到停止．学员乙记录下自己经过B、C杆时的时刻tB=4.50s，tC=6.50s．已知LOA=44m．求：
19．
如图所示，一理想变压器原、副线圈接有两只电阻R1和R2，R1=R2=4Ω，原线圈匝数是副线圈匝数的5倍，当原线圈接在某正弦交变电源上时，变压器的输出功率是100W，则（ ）
如图所示，一理想变压器原、副线圈接有两只电阻R1和R2，R1=R2=4Ω，原线圈匝数是副线圈匝数的5倍，当原线圈接在某正弦交变电源上时，变压器的输出功率是100W，则（ ）| A． | 交流电源的输出功率等于100W | |
| B． | 交流电源的输出电流等于1A | |
| C． | R2两端电压是R1两端电压的5倍 | |
| D． | 原线圈所接电源电压是R2两端电压的5倍 |