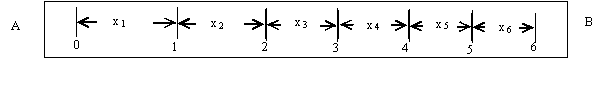题目内容
如图11所示，物体A放在足够长的木板B上，木板B静止于水平面。已知A的质量mA和B的质量mB均为2.0kg，A、B之间的动摩擦因数μ1=0.2，B与水平面之间的动摩擦因数μ2=0.1，最大静摩擦力与滑动摩擦力大小视为相等，重力加速度g取10m/s2。若t=0开始，木板B受F1=16N的水平恒力作用，t=1s时F1改为F2=4N，方向不变，t=3s时撤去F2。
（1）木板B受F1=16N的水平恒力作用时，A、B的加速度aA、aB各为多少？
（2）从t=0开始，到A、B都静止，A在B上相对B滑行的时间为多少？
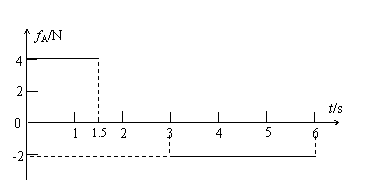
（3）请以纵坐标表示A受到B的摩擦力fA，横坐标表示运动时间t（从t=0开始，到A、B都静止），取运动方向为正方向，在图12中画出fA—t的关系图线（以图线评分，不必写出分析和计算过程）。
 |
 |
（1）(5分)
根据牛顿第二定律得
μ1mAg=mAaA --------------------------------------①----------------（1分）
aA=μ1g
=0.2×10m/s2
=2 m/s2 ----------------------------------------------②----------------（1分）
F1－μ2(mA+mB) g－μ1mAg=mBaB ------------------③----------------（2分）
代入数据得
aB=4 m/s2 --------------------------------④-----------------（1分）
（2）(9分)
t1=1s时，A、B分别为vA、vB
vA= aA t1 ------------------------------------------------⑤-----------------（1分）
=2×1 m/s
=2 m/s ----------------------------------------⑥-----------------（1分）
vB= aB t1 -------------------------------------------------⑦-----------------（1分）
=4×1 m/s
=4 m/s ---------------------------------------⑧------------------（1分）
F1改为F2=4N后，在B速度大于A速度的过程，A的加速度不变，B的加速度设为
， 根据牛顿第二定律得
F2－μ2(mA+mB) g－μ1mAg=mB -------------------⑨---------------（1分）
代入数据得
=－2m/s2 ---------------------------------------⑩----------------（1分）
设经过时间t2，A、B速度相等，此后它们保持相对静止。
vA + aA t2= vB+t2 ------------------------------------⑾…-------------（1分）
代入数据得t2=0.5s -------------------------⑿---------------（1分）
A在B上相对B滑行的时间为t= t1+ t2=1.5s--------⒀---------------（1分）
（3）（6分）
 |
如图11所示，光滑弧形轨道下端与水平传送带上表面等高，轨道上的A点到传送带的竖直距离和传送带上的表面到地面的距离为均为h=5m，把一物体放在A点由静止释放，当传送带不动，物体从右端B点水平飞记，落在水平地面上的P点，B、P的水平距离OP为x=2m．g取10m/s2，求：
