Question

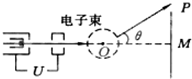电视机的显像管中，电子束的偏转是用磁偏转技术实现的．电子束经过加速电场后，进入一圆形匀强磁场区，磁场方向垂直于圆面．不加磁场时，电子束将通过磁场中心O点而打到屏幕上的中心M，加磁场后电子束偏转到P点外侧．现要使电子束偏转回到P点，可行的办法是（　　）

• A、增大加速电压
• B、增加偏转磁场的磁感应强度
• C、将圆形磁场区域向屏幕远离些
• D、将圆形磁场的半径增大些

Answer 1

分析：由动能定理得到电子获得的速度与加速电压的关系．电子进入磁场后由洛伦兹力提供向心力，根据牛顿第二定律得到半径与速度的关系，联立得到半径与加速的电压的关系．根据几何知识分析得知，要使电子束偏转回到P点，要减小电子经过磁场后的偏转角度，由电子的轨迹半径与磁场半径的关系分析所采用的方法．

解答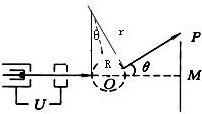：解：电子在加速电场中：根据动能定理得：
qU=

1

2

mv²，
得到：v=

2qU m

=

2eU m

电子进入磁场过程中，由evB=

mv2

r

得电子的轨迹半径为：r=

mv

eB

=

m

eB

2eU m

设磁场的半径为R，电子经过磁场后速度的偏向角为θ，根据几何知识得：tan

θ

2

=

R

r

A、增大加速电压U时，由上可知，r增大，θ减小，可使电子束偏转回到P点．故A正确．
B、增加偏转磁场的磁感应强度B时，r减小，θ增大，电子向上偏转，不能使电子束偏转回到P点．故B错误．
C、将圆形磁场区域向屏幕远离些时，电子的偏向角不变，根据几何知识可知，电子束偏转位移更多，不可能回到P点．故C错误．
D、将圆形磁场的半径增大些时，r不变，θ增大，电子向上偏转，不能使电子束偏转回到P点．故D错误．
故选：A

点评：带电粒子的加速过程，根据动能定理求粒子得到的速度，带电粒子在磁场中根据牛顿第二定律求半径，由几何知识分析偏转角度，都是基本的思路．