题目内容
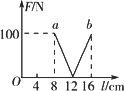
一个质量可以不计的弹簧，其弹力F的大小与长度l的关系如图中的直线a、b所示，这根弹簧的劲度系数为
[ ]
A．
1 250 N/m
B．
625 N/m
C．
2 500 N/m
D．
833 N/m
答案：C
解析：
解析：
|
由图象可以看出在直线a对应的阶段，弹簧处于压缩状态，弹力F随着缩短量的减小而减小，当弹簧长度为12 cm时恢复原长；直线b对应的是弹簧的伸长阶段，弹力F随伸长量的增大线性递增．由此可看出当弹力F＝100 N时，弹簧对应的形变量x＝4 cm，根据胡克定律可求出弹簧的劲度系数k＝ |
＝2 500 N/m．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
（2008?茂名模拟）在纳米技术中需要移动或修补原子，必须使在不停地做热运动（速率约几百米每秒）的原子几乎静止下来且能在一个小的空间区域内停留一段时间，为此已发明了“激光制令”的技术，若把原子和入射光分别类比为一辆小车和一个小球，则“激光制冷”与下述的力学模型很类似．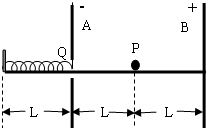
如图所示，A、B是两块竖直放置的平行金属板，相距为2L，分别带有等量的负、正电荷，在两板间形成电场强度大小为E的匀强电场．A板上有一小孔（它的存在对两板间匀强电场分布的影响可忽略不计），孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道，一个质量为m，电荷量为g（g＞0）的小球（可视为质点），在外力作用下静止在轨道的中点P处．孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道，轨道上距A板L处有一固定档板，长为L的轻弹簧左端固定在挡板上，右端固定一块轻小的绝缘材料制成的薄板Q．撤去外力释放带电小粒，它将在电场力作用下由静止开始向左运动，穿过小孔后（不与金属板A接触）与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能．小球从接触Q开始，经历时间To第一次把弹簧压缩至最短，然后又被弹簧弹回．由于薄板Q的绝缘性能有所欠缺，使得小球每次离开Q瞬间，小球的电荷量都损失一部分，而变成刚与Q接触时小球电荷量的