题目内容
如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v。水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R="2.5" m的圆截去了左上角l270的圆弧,CB为其竖直直径,(sin530="0.8" cos530=0.6,重力加速度g取10m/s2)求:
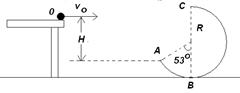
(1) 小球经过C点的速度大小;
(2) 小球运动到轨道最低点B时小球对轨道的压力大小;
(3) 平台末端O点到A点的竖直高度H。
【答案】
(1)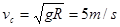 (2)6.0N(3)3.36m
(2)6.0N(3)3.36m
【解析】
试题分析:(1)恰好运动到C点,有重力提供向心力,即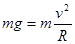 1分
1分
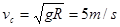 1分
1分
(2)从B点到C点,由动能定理有: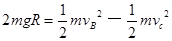 1分
1分
在B点对小球进行受力分析,由牛顿第二定律有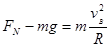 1分
1分
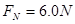 1分
1分
根据牛顿第三定律,小球对轨道的压力大小为6.0N 1分
(3)从A到B由动能定理有: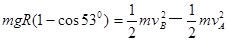 1分
1分
所以: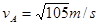 1分
1分
在A点进行速度的分解有: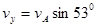 1分
1分
所以: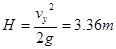 1分
1分
考点:机械能守恒定律;牛顿第二定律;
点评:本题是平抛运动和圆周运动相结合的典型题目,除了运用平抛运动和圆周运动的基本公式外,求速度的问题,动能定理不失为一种好的方法.

练习册系列答案
相关题目
 如图所示,将一质量为m的小球从空中O点以速度v0水平抛出,飞行一段时间后,小球经过空间P点时动能为Ek,不计空气阻力,则下列结论不正确的是( )
如图所示,将一质量为m的小球从空中O点以速度v0水平抛出,飞行一段时间后,小球经过空间P点时动能为Ek,不计空气阻力,则下列结论不正确的是( )A、小球经过P点时竖直分速度为
| ||||||||
B、从O点到P点,小球的高度下降
| ||||||||
C、从O点到P点过程中,小球运动的平均速度为
| ||||||||
D、从O点到P点过程中,小球运动的平均速度为
|
 如图所示,将一质量为m的摆锤用长为L的细绳吊起,上端固定,使摆锤在水平面内做匀速圆周运动,细绳就沿圆锥面旋转,构成一个大型圆锥摆,如果细绳与竖直方向夹角为θ,已知L=5m,r=3m,求这个圆锥摆的周期(保留一位有效数字).
如图所示,将一质量为m的摆锤用长为L的细绳吊起,上端固定,使摆锤在水平面内做匀速圆周运动,细绳就沿圆锥面旋转,构成一个大型圆锥摆,如果细绳与竖直方向夹角为θ,已知L=5m,r=3m,求这个圆锥摆的周期(保留一位有效数字). (2011?徐州一模)如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v.水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,CB为其竖直直径,(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)求:(1)小球经过C点的速度大小;
(2011?徐州一模)如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v.水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,CB为其竖直直径,(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)求:(1)小球经过C点的速度大小; 如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆,下列说法中正确的是( )
如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆,下列说法中正确的是( )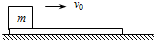 如图所示,将一质量为3m的长木板静止地放在水平面上,另一质量为m的木块以水平初速度v0滑上长木板,若木块与木板、木板与桌面间的动摩擦因数均为μ,则在木块与长木板相对静止之前,长木板受桌面的摩擦力大小为( )
如图所示,将一质量为3m的长木板静止地放在水平面上,另一质量为m的木块以水平初速度v0滑上长木板,若木块与木板、木板与桌面间的动摩擦因数均为μ,则在木块与长木板相对静止之前,长木板受桌面的摩擦力大小为( )