题目内容
 如图所示,将一质量为m的摆锤用长为L的细绳吊起,上端固定,使摆锤在水平面内做匀速圆周运动,细绳就沿圆锥面旋转,构成一个大型圆锥摆,如果细绳与竖直方向夹角为θ,已知L=5m,r=3m,求这个圆锥摆的周期(保留一位有效数字).
如图所示,将一质量为m的摆锤用长为L的细绳吊起,上端固定,使摆锤在水平面内做匀速圆周运动,细绳就沿圆锥面旋转,构成一个大型圆锥摆,如果细绳与竖直方向夹角为θ,已知L=5m,r=3m,求这个圆锥摆的周期(保留一位有效数字).分析:向心力是根据效果命名的力,可以是几个力的合力,也可以是某个力的分力,对物体受力分析时不能把向心力作为一个力分析,摆球只受重力和拉力作用;摆球做圆周运动所需要的向心力是重力沿水平方向指向圆心的分力提供的,即F1=mgtanθ=m(
)2r=mω2(Lsinθ),可以求出T.
| 2π |
| T |
解答: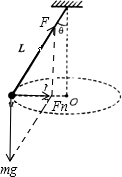 解:如图所示,球受重力、拉力作用做圆周运用.
解:如图所示,球受重力、拉力作用做圆周运用.
令悬挂点为A,由几何关系可得:OA=4m
Fn=mgtanθ=m(
)2r
又tanθ=
代入数据解得:T=4s
答:这个圆锥摆的周期为4s.
 解:如图所示,球受重力、拉力作用做圆周运用.
解:如图所示,球受重力、拉力作用做圆周运用.令悬挂点为A,由几何关系可得:OA=4m
Fn=mgtanθ=m(
| 2π |
| T |
又tanθ=
| 3 |
| 4 |
代入数据解得:T=4s
答:这个圆锥摆的周期为4s.
点评:此题要知道向心力的含义,能够分析向心力的来源,知道向心力可以是几个力的合力,也可以是某个力的分力,此题中重力沿着水平方向的分力提供力小球做圆周运动所需的向心力.此题有一定的难度,属于中档题.

练习册系列答案
相关题目
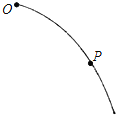 如图所示,将一质量为m的小球从空中O点以速度v0水平抛出,飞行一段时间后,小球经过空间P点时动能为Ek,不计空气阻力,则下列结论不正确的是( )
如图所示,将一质量为m的小球从空中O点以速度v0水平抛出,飞行一段时间后,小球经过空间P点时动能为Ek,不计空气阻力,则下列结论不正确的是( )A、小球经过P点时竖直分速度为
| ||||||||
B、从O点到P点,小球的高度下降
| ||||||||
C、从O点到P点过程中,小球运动的平均速度为
| ||||||||
D、从O点到P点过程中,小球运动的平均速度为
|
 (2011?徐州一模)如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v.水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,CB为其竖直直径,(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)求:(1)小球经过C点的速度大小;
(2011?徐州一模)如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v.水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,CB为其竖直直径,(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)求:(1)小球经过C点的速度大小; 如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆,下列说法中正确的是( )
如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆,下列说法中正确的是( )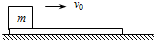 如图所示,将一质量为3m的长木板静止地放在水平面上,另一质量为m的木块以水平初速度v0滑上长木板,若木块与木板、木板与桌面间的动摩擦因数均为μ,则在木块与长木板相对静止之前,长木板受桌面的摩擦力大小为( )
如图所示,将一质量为3m的长木板静止地放在水平面上,另一质量为m的木块以水平初速度v0滑上长木板,若木块与木板、木板与桌面间的动摩擦因数均为μ,则在木块与长木板相对静止之前,长木板受桌面的摩擦力大小为( )