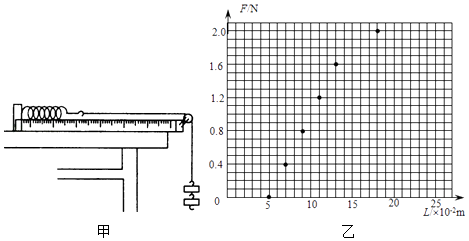
��Ŀ����
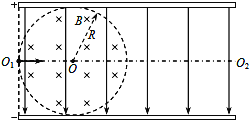
����Ŀ����ͼ��ʾ������ƽ�н��������Ϊ2R���������뾶ΪR��Բ���������д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB�����弰������Ե���߾���ų��߽�պ����У�һ���ӣ������������������������O1O2�����O1����ijһ�ٶ����룬��ֱ��ͨ��Բ�δų�����Ȼ��ǡ�ôӼ����Ե�ɳ����ڼ�����˶�ʱ��Ϊt0��������ȥ�ų��������Դ�O1������ͬ�ٶ����룬��t0/2ʱ������ϣ�
��1������������ѹU��
��2�������ӴӼ����ɳ�ʱ���ٶȴ�С��
��3���������岻���磬���ִų����䣬��������������O1O2�����O1�����룬��ʹ���Ӵ���������ɳ���������ٶ�Ӧ����ʲô������
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��
����������1�������Ӵ����O1��������ٶ�Ϊ![]() �����峤Ϊ
�����峤Ϊ![]()
�ڸ��ϳ����������˶��� ![]() ��2�֣�
��2�֣�
�ڵ糡������ƽ���˶��� ![]()
![]() ��2�֣�
��2�֣�
��![]() ��1�֣�
��1�֣�
��ȥ�ų������ܵ糡�����У� ![]() ��1�֣�
��1�֣�
���![]()
![]()
![]()
![]() ��2�֣�
��2�֣�
��2�����ӴӼ����ɳ�ʱ���ص糡������ٶȴ�С![]()
![]()
![]()
![]()
![]() ��1�֣�
��1�֣�
�Ӽ����ɳ�ʱ���ٶȴ�С![]()
![]() ��1�֣�
��1�֣�
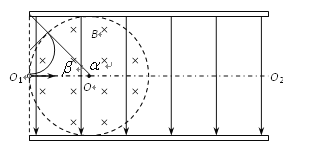
��3���������ڴų�����Բ���˶��Ĺ���뾶Ϊr������ǡ�ô��ϼ������Ե�ɳ�ʱ�ٶȵ�
ƫת��Ϊ![]() ���ɼ��ι�ϵ��֪��
���ɼ��ι�ϵ��֪�� ![]()
![]() ��r+
��r+![]() r=R��2�֣�
r=R��2�֣�
��Ϊ![]() ������
������![]() ��1�֣�
��1�֣�
������������ʽ![]() �����v=
�����v=![]() ��2�֣�
��2�֣�
���ԣ����Ӵ���������ɳ�������Ϊ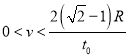 ��1�֣�
��1�֣�