题目内容
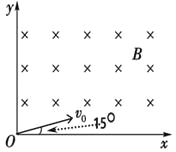
【题目】如图，三角形AOB为等腰直角三棱镜的横截面，以OA、OB为轴建立直角坐标系xOy，OA＝OB＝L，棱镜的折射率为n＝
。一束平行于斜边AB的平行光从OB边射入。光透过棱镜只考虑一次内部反射。
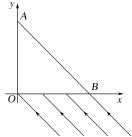
(1)求距离O点多远的入射光刚好从A点射出；
(2)部分光将会从OA边以平行于AB边的方向射出，这部分透射光在垂直于光线方向的宽度。(已知sin15°＝
，cos15°＝
)
【答案】（1）
L（2）
L
【解析】
（1）作出光路图，根据折射定律求出sini与sinr之间的定量关系，由三角函数关系求出即可．
（2）由于题目平行于AB的方向入射，平行于AB的方向出射，光线在AB中的传播具有一定的对称性，结合该对称性与光路图，以及相应的几何关系即可求出．
（1）设光线从C点射入刚好从A点射出，入射角与折射角分别为α和β，由折射定律知：
所以：
所以：β=30°
所以：OC＝AOtan30°＝L
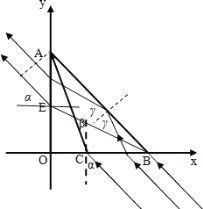
（2）根据题意光线经过AB边全反射后从OA边AE段射出，结合光路图可知，BC之间的光线能经AB全反射后从AO之间射出．设光线宽度为d，由几何关系可知，光射到AB界面上后的入射角：γ=90°-[180°-45°-（90°+β）]=75°
而光在介质中的临界角为C，有：
，所以C=45°＜75°
光线在AB的界面上发生全反射，BC的宽度为：BC＝OBOC＝LL
根据光路可逆可得：AE=BC=LL
光线的宽度为：d=AEsin45°= L
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
