题目内容
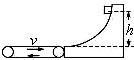
（14分）如图所示，半径R = 0.1m的竖直半圆形光滑轨道bc与水平面ab相切。质量m = 0.1kg的小滑块B放在半圆形轨道末端的b点，另一质量也为m= 0.1kg的小滑块A，以v0 = 2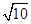
m/s的水平初速度向B滑行，滑过s = 1m的距离，与B相碰，碰撞时间极短，碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
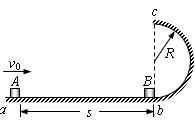
（1）A与B碰撞前瞬间的速度大小vA；
（2）碰后瞬间，A、B共同的速度大小v；
（3）在半圆形轨道的最高点c，轨道对A、B的作用力N的大小。
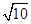m/s的水平初速度向B滑行，滑过s = 1m的距离，与B相碰，碰撞时间极短，碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求 （1）A与B碰撞前瞬间的速度大小vA；
（2）碰后瞬间，A、B共同的速度大小v；
（3）在半圆形轨道的最高点c，轨道对A、B的作用力N的大小。
（1）6m/s；（2）3m/s；（3）8N
试题分析：（1）滑块从a向b运动过程中，根据动能定理
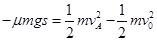
可知
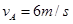
（2）A、B碰撞过程中，满足动量守恒
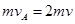
得
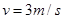
（3）从b到c过程中，机械能守恒
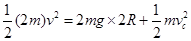
在C点时
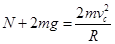
得：轨道对A、B的作用力N=8N
练习册系列答案
阅读快车系列答案
相关题目
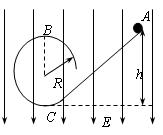
．一质量也为m的小球A从左侧的最高点自由滑下，A滑到水平面与B碰后立即粘在一起结合成D就不再分离（碰撞时间极短）．当D、C一起刚要滑到右侧最低点时，弹簧锁定解除且立即将C弹出并与弹簧分离．求
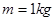，半径分别为
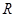和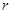
，两板之间用一根长
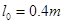的轻绳将薄板中心相连结（未画出）.开始时，两板水平放置并叠合在一起，静止于距离固定支架C高度
处. 然后自由下落到C上，支架上有一半径为
(
)的圆孔，圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞（碰撞时间极短）. 碰撞后，两板即分离，直到轻绳绷紧.在轻绳绷紧的瞬间，两板立即具有共同速度.不计空气阻力，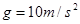
，求：
的N点时速度恰好为零．（重力加速度为g）
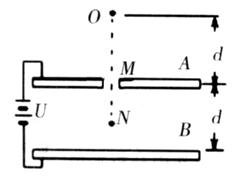
的距离．质点仍从O点由静止自由下落，求质点下落速度为零时距B板的距离．