Question

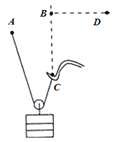
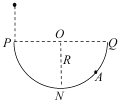
【题目】如图所示，一半径为R、粗糙程度处处相同的半圆形轨道竖直固定放置，直径POQ水平。轨道上的A点离PQ的距离为，一质量为m的质点自P点正上方距离P点高h=2R由静止释放，进入轨道后刚好能到达Q点并能再次返回经过N点．已知质点第一次滑到轨道最低点N时速率为v1，第一次到达A点时速率为v2，选定N点所在的水平面为重力势能的零势能面，重力加速度为g，则

A.

B.

C. 从N到Q的过程中，动能与势能相等的点在A点上方，从Q到N的过程中，动能与势能相等的点在A点下方

D. 从N到Q的过程中，动能与势能相等的点在A点下方，从Q到N的过程中，动能与势能相等的点在A点上方

Answer 1

【答案】BC

【解析】

设质点到达P点时的速度为v，根据动能定理有mg2R＝mvP20；解得；由题意由静止释放刚好能达到Q点，由动能定理有mg2RWf＝00得Wf＝2mgR；因为从P到N每个点速度均大于N到Q每个点的速度，P到N的正压力大于N到Q，P到N的摩擦力大于N到Q的摩擦力，所以P到N克服摩擦力做功大于mgR，由P到N由动能定理得mgR Wf＝＜0，所以，即第一次滑到轨道最低点时的速率，故B正确。如果轨道光滑，物体在运动过程中不受摩擦力，上升过程中动能与重力势能相等的位置在位移的中点A，现在由于要克服摩擦力做功，机械能减小，所以上升过程中动能与重力势能相等的位置在A点上方，从Q到N的过程中，动能与势能相等的点在A点下方。故C正确；故选BC。