题目内容
（1）如图所示，质量为m1和m2的两物体分别系在细绳的两端，绳跨在光滑的定滑轮，AB段恰好水平，两物体置于光滑斜面上，且均处于静止状态，则m1对斜面的压力等于多少？
（2）在（1）问图示中，若斜面倾角为θ（θ＜45°），斜面上物体质量为m1，且物体与斜面间的动摩擦因数为μ0，为使物体能静止在斜面上，定滑轮所吊物体m2的质量为多大？（轮光滑，且质量不计，绳质量也不计，最大静摩擦力等于滑动摩擦力．μ0＜tgθ）
解：（1）对m1受力分析：
其中T与m1g正交，且 T=m2g
∴FN=
=g
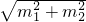
由牛顿第三定律知：斜面所受压力 Q=FN=g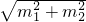
（2）当m2最小时，m1受力分析如图：
有：FN=m1gcosθ+m2gsinθ
m1gsinθ=μ0FN′+m2gcosθ
解得：m2=
m1
当m2最大时，对m1受力分析：
有：FN′=m1gcosθ+m2gsinθ
m1gsinθ+μ0FN′=m2gcosθ
联立得：m2=m1
所以使m1静止，m2的取值是：m1≤m2≤m1
答：（1）斜面所受压力 为g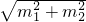
（2）使m1静止，m2的取值是：m1≤m2≤m1．
分析：（1）对m1受力分析根据平衡条件即可求解
（2）当静摩擦力沿斜面向下时有m2的最小值，当摩擦力沿斜面向上时有m2的最大值
点评：本题的难度来自于静摩擦力的可变化性，先找到临界情况后求极值．难点在于表达式繁琐，书写时要认真．
其中T与m1g正交，且 T=m2g
∴FN=
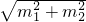
=g 由牛顿第三定律知：斜面所受压力 Q=FN=g
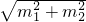
（2）当m2最小时，m1受力分析如图：
有：FN=m1gcosθ+m2gsinθ
m1gsinθ=μ0FN′+m2gcosθ
解得：m2=
m1 当m2最大时，对m1受力分析：
有：FN′=m1gcosθ+m2gsinθ
m1gsinθ+μ0FN′=m2gcosθ
联立得：m2=m1
所以使m1静止，m2的取值是：
m1≤m2≤m1 答：（1）斜面所受压力 为g
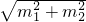
（2）使m1静止，m2的取值是：
m1≤m2≤m1．分析：（1）对m1受力分析根据平衡条件即可求解
（2）当静摩擦力沿斜面向下时有m2的最小值，当摩擦力沿斜面向上时有m2的最大值
点评：本题的难度来自于静摩擦力的可变化性，先找到临界情况后求极值．难点在于表达式繁琐，书写时要认真．
练习册系列答案
相关题目
（1）如图所示，质量为20g的子弹，以300m/s的速度水平射入厚度是10cm的木板，射穿后的速度是100m/s．子弹在射穿木板的过程中所受的平均阻力是
（1）如图所示，质量与身高均相同的甲、乙两人分别乘坐速度为0.6c和0.8c（c为光速）的飞船同向运动．则下列说法中正确的是 
| A．乙观察到甲身高变高 |
| B．甲观察到乙身高不变 |
| C．若甲向乙挥手，则乙观察到甲动作变快 |
| D．若甲向乙发出一束光进行联络，则乙观察到该光束的传播速度为0.2c |
时刻的波形图．已知
，若波速为15m/s，则质点M在t时刻的振动方向为 ；则在
时间内，质点M通过的路程为 m． 
（3）某同学用如图所示装置测量某种液体的折射率，首先在紧贴着容器边缘竖直插入一根长刻度尺，零刻度线在A端，当容器中没有液体时，该同学在图示位置只能看到标尺上的P点，当容器中正好装满液体时，刚好观察到零刻度线，已知圆柱形容器的直径d=12cm，高h=16cm，P点的刻度值L=7cm，求该透明液体的折射率．
时刻的波形图．已知
，若波速为15m/s，则质点M在t时刻的振动方向为 ；则在
时间内，质点M通过的路程为 m． 
