题目内容
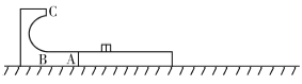
【题目】如图所示，固定光滑轨道ABC的AB段水平，BC段为半圆形，B是半圆轨道的最低点、C是半圆轨道的最高点。长L=1.5m、质量M=0.4kg的木板位于足够长的光滑水平面上，木板左端紧靠A点，上表面与AB等高。将质量均为m=0.2kg的小滑块甲、乙放置在木板上距A点0.5m处，甲、乙之间夹有被压缩的轻质短弹簧。某时刻弹簧弹开，甲向左运动，乙恰好未从木板上滑下，已知甲、乙与木板间的动摩擦因数均为
，重力加速度g=10m/s2。
(1)求甲到达A点时的速度大小；
(2)若甲能通过半圆轨道的C点且整个过程中对轨道的压力不超过20N，求轨道BC半径的取值范围；
(3)若在水平面与木板间固定一块桌布，木板与桌布间的动摩擦因数
，求乙滑下木板时的速度。
【答案】(1)
；(2)
；(3)
【解析】
(1)弹簧弹开，以甲、乙组成系统为研究对象，在甲到达A点之前，系统动量守恒
甲、乙对车的摩擦力大小相等、方向相反，故车保持静止。当甲到达A点时乙距木板右端距离为
，此后以乙和木板为研究对象，乙到达木板右端时两者同速，设为v，由动量守恒得
由能量守恒得
联立解得
(2)半圆轨道半径最大时甲恰能通过半圆轨道最高点
甲在B点对轨道的压力最大，且半径越小压力越大，半径最小时，由牛顿第三定律知轨道对乙的最大作用力
则半径的取值范围
代入解得
(3)甲离开木板后，对乙
对板
联立解得
练习册系列答案
相关题目
