题目内容
1.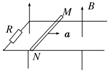 如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=1m,左端接有阻值R=0.9Ω的电阻.一质量m=1kg、电阻r=0.1Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=1T.金属棒在水平向右的外力作用下,由静止开始以a=5m/s2的加速度做匀加速运动,当金属棒的位移x=10m时撤去外力,金属棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q1:Q2=5:1.导轨足够长且电阻不计,金属棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求:
如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=1m,左端接有阻值R=0.9Ω的电阻.一质量m=1kg、电阻r=0.1Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=1T.金属棒在水平向右的外力作用下,由静止开始以a=5m/s2的加速度做匀加速运动,当金属棒的位移x=10m时撤去外力,金属棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q1:Q2=5:1.导轨足够长且电阻不计,金属棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求:(1)金属棒在匀加速运动过程中,通过电阻R的电荷量q;
(2)撤去外力后导体棒克服磁场力做的功W;
(3)外力做的功WF.
分析 (1)根据运动学公式求出时间,根据电量的公式求解
(2)撤去外力后棒在安培力作用下做减速运动,安培力做负功先将棒的动能转化为电能,再通过电流做功将电能转化为内能,所以焦耳热等于棒的动能减少.
(3)根据动能定理求解
解答 解:(1)棒匀加速运动所用时间为t,有:$\frac{1}{2}$at2=x
t=$\sqrt{\frac{2x}{a}}$=$\sqrt{\frac{2×10}{5}}$=2s
根据法拉第电磁感应定律和闭合电路的欧姆定律求电路中产生的平均电流为:$\overline{I}$=$\frac{\overline{E}}{R+r}$=$\frac{△∅}{t(R+r)}$
根据电流定义式有:
q=$\overline{I}$t=$\frac{△∅}{R+r}$=$\frac{BLx}{R+r}$=$\frac{1×1×10}{0.9+0.1}$=10C
(2)撤去外力前棒做匀加速运动根据速度公式末速为:
v=at=2×5=10m/s
撤去外力后棒在安培力作用下做减速运动,安培力做负功先将棒的动能转化为电能,
再通过电流做功将电能转化为内能,所以焦耳热等于棒的动能减少.
Q2=△EK=$\frac{1}{2}$mv2=$\frac{1}{2}×1×1{0}^{2}$=50J
(3)根据题意在撤去外力前的焦耳热为:
Q1=5Q2=250J
撤去外力前拉力做正功、安培力做负功(其绝对值等于焦耳热Q1)、重力不做功共同使棒的动能增大,
根据动能定理有:
△EK=WF-Q1
则:WF=△EK+Q1=300J
答:(1)棒在匀加速运动过程中,通过电阻R的电荷量是10C;
(2)撤去外力后回路中产生的焦耳热是50J;
(3)外力做的功是300 J
点评 解决该题关键要分析物体的运动情况,清楚运动过程中不同形式的能量的转化,知道运用动能定理求解变力做功.

 名师点拨卷系列答案
名师点拨卷系列答案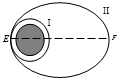 信使号水星探测器按计划将在今年陨落在水星表面.工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
信使号水星探测器按计划将在今年陨落在水星表面.工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )| A. | 探测器在轨道Ⅰ上E点速率等于在轨道Ⅱ上E点速率 | |
| B. | 探测器在轨道Ⅱ上某点的速率可能等于在轨道Ⅰ上速率 | |
| C. | 探测器在轨道Ⅰ和轨道Ⅱ上的E处加速度相同 | |
| D. | 探测器在轨道Ⅱ上远离水星过程中,势能和动能均减少 |
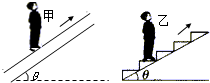
| A. | 甲受到扶梯的摩擦力,乙不受摩擦力 | |
| B. | 扶梯对甲乙的弹力相同 | |
| C. | 扶梯对甲乙的弹力与甲乙的重力大小相等 | |
| D. | 斜面对甲乙都不做功 |
| A. | 它们做圆周运动的万有引力保持不变 | |
| B. | 它们做圆周运动的角速度不变 | |
| C. | 体积较大星体圆周运动轨迹半径不变,线速度也不变 | |
| D. | 体积较大星体圆周运动轨迹半径变大,线速度变小 |
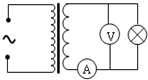 如图所示,绕组线圈电阻不可忽略的变压器,接电动势e=220$\sqrt{2}$sin100πt(V)的正弦交流电,副线圈接有理想电流表、理想电压表和一只“110V,60W”的灯泡,已知变压器原、副线圈匝数比为2:1,下列说法正确的是( )
如图所示,绕组线圈电阻不可忽略的变压器,接电动势e=220$\sqrt{2}$sin100πt(V)的正弦交流电,副线圈接有理想电流表、理想电压表和一只“110V,60W”的灯泡,已知变压器原、副线圈匝数比为2:1,下列说法正确的是( )| A. | 副线圈产生的电动势的有效值为110V | |
| B. | 电压表读数为110V | |
| C. | 灯泡能正常发光 | |
| D. | 变压器的输出功率小于输入功率 |
| A. | 两卫星最终的运行轨道不同 | |
| B. | 发射两卫星消耗的能量不同 | |
| C. | 两卫星的线速度都大于7.9km/s | |
| D. | 两卫星的线速度与地球赤道表面上的线速度相同 |
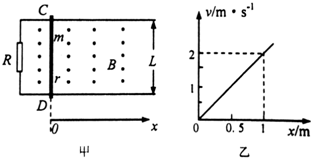 如图甲所示,左侧接有定值电阻R=2Ω的水平粗糙导轨处于垂直纸面向外的匀强磁场中,磁感应强度B=1T,导轨间距L=1m.-质量m=2kg,阻值r=2Ω的金属棒在水平拉力F作用下由静止开始从CD处沿导轨向右加速运动,金属棒的v-x图象如图乙所示,若金属棒与导轨间动摩擦因数μ=0.25,则从起点发生x=1m位移的过程中(g=10m/s2)( )
如图甲所示,左侧接有定值电阻R=2Ω的水平粗糙导轨处于垂直纸面向外的匀强磁场中,磁感应强度B=1T,导轨间距L=1m.-质量m=2kg,阻值r=2Ω的金属棒在水平拉力F作用下由静止开始从CD处沿导轨向右加速运动,金属棒的v-x图象如图乙所示,若金属棒与导轨间动摩擦因数μ=0.25,则从起点发生x=1m位移的过程中(g=10m/s2)( )| A. | 金属棒克服安培力做的功W1=0.5J | B. | 金属棒克服摩擦力做的功W2=4J | ||
| C. | 整个系统产生的总热量Q=4.25J | D. | 拉力做的功W=9.25J |