如图所示.在平面直角坐标系xOy的第一象限内分布有方向竖直向下.宽度为2d的匀强电场.一质量为m.电荷量为+q的带电粒子从y轴上的A点以速度v0水平向右射出.穿过匀强电场后恰好打在x轴上的G点.且速度方向与x轴正方向成θ=60°夹角斜向下．若A点坐标为.G点坐标为.粒子重力不计．(1)试求该匀强电场的电场强度E的大小,(2)若撤去电场.在该坐标系的第一象限内� 题目和参考答案——青夏教育精英家教网—

题目内容

7．

如图所示，在平面直角坐标系xOy的第一象限内分布有方向竖直向下、宽度为2d的匀强电场，一质量为m、电荷量为+q的带电粒子从y轴上的A点以速度v₀水平向右射出，穿过匀强电场后恰好打在x轴上的G点，且速度方向与x轴正方向成θ=60°夹角斜向下．若A点坐标为（0，2$\sqrt{3}$d），G点坐标为（3d，0），粒子重力不计．
（1）试求该匀强电场的电场强度E的大小；
（2）若撤去电场，在该坐标系的第一象限内加上一个方向垂直纸面向外、磁感应强度大小为B的圆形磁场，粒子扔按原方向入射，经磁场偏转后粒子仍打在x轴上的G点，且速度方向与x轴正方向成θ=60°夹角斜向下，试求该圆形磁场的最小面积S．

分析（1）粒子垂直于电场进入电场，在电场中粒子做类平抛运动，由运动的分解求出粒子到达电场的边界时的位置，再用平抛运动的公式即可求出电场强度．
（2）粒子以此速度进入第四象限，在洛伦兹力的作用下做匀速圆周运动，利用洛伦兹力提供向心力的公式，可由牛顿第二定律求出在磁场中运动的半径r，然后结合几何关系判断出磁场的最小半径和最小面积．

解答解：（1）粒子沿与x轴正方向成θ=60°夹角斜向下穿过x轴如图，可知：

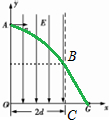
$\frac{\overline{BC}}{\overline{CG}}=tan60°=\sqrt{3}$
所以：$\overline{BC}=\sqrt{3}\overline{CG}=\sqrt{3}×（3d-2d）=\sqrt{3}d$
粒子在电场中做平抛运动，水平方向：2d=v₀t
竖直方向：$（2\sqrt{3}d-\sqrt{3}d）=\frac{1}{2}a{t}^{2}$
其中：$a=\frac{qE}{m}$
联立得：E=$\frac{\sqrt{3}m{v}_{0}^{2}}{2qd}$
（2）粒子在磁场中运动时洛伦兹力提供向心力，所以：
$q{v}_{0}B=\frac{m{v}_{0}^{2}}{r}$
得：$r=\frac{m{v}_{0}}{qB}$
又由题意，粒子在磁场中偏转的角度是60°，则在磁场中运动的轨迹如图：

由图可知当粒子的入射点与出射点的连线恰好是磁场的直径时，磁场的面积最小．此时：
$\frac{R}{r}=sin\frac{60°}{2}=sin30°=0.5$
所以：R=0.5r
所以磁场的最小面积：S=πR²=$\frac{π{m}^{2}{v}_{0}^{2}}{{4q}^{2}{B}^{2}}$
答：（1）该匀强电场的电场强度E的大小是$\frac{\sqrt{3}m{v}_{0}^{2}}{2qd}$；
（2）该圆形磁场的最小面积是$\frac{π{m}^{2}{v}_{0}^{2}}{{4q}^{2}{B}^{2}}$．