题目内容
20. 汽车在水平路面做半径为R的大转弯,图是后视图,悬吊在车顶的灯左偏了θ角,则:
汽车在水平路面做半径为R的大转弯,图是后视图,悬吊在车顶的灯左偏了θ角,则:(1)车正向左转弯还是向右转弯?
(2)车速是多少?
(3)若(2)中求出的速度正是汽车转弯时不打滑允许的最大速度,则车轮与地面的动摩擦因数μ是多少?
分析 灯加速度与汽车的向心加速度相同,对灯受力分析,根据牛顿第二定律列式求解向心力,根据向心力公式列式求解.
汽车沿圆跑道行驶时,由静摩擦力提供向心力,当静摩擦力达到最大值时,车速达到最大,由牛顿第二定律求出动摩擦因数.
解答 解:(1)灯加速度与汽车的向心加速度相同,对灯受力分析,受重力和拉力,灯的合力向右,提供向心力,所以车正向右转弯.
(2)根据牛顿第二定律,有:
F合=mgtanθ=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{gRtanθ}$,
(3)以汽车为研究对象,当汽车受到的静摩擦力达到最大值时速度达到最大,设最大速度为vm.
根据牛顿第二定律得:μmg=mgtanθ
μ=tanθ
答:(1)车正向右转弯
(2)车速是$\sqrt{gRtanθ}$,
(3)若(2)中求出的速度正是汽车转弯时不打滑允许的最大速度,则车轮与地面的动摩擦因数μ是tanθ.
点评 本题关键是明确灯加速度与汽车的向心加速度相同,然后对灯受力分析,结合牛顿第二定律和向心力公式列式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在漫长的人类发展历程中,有许多科学家在物理学研究上做出了突出的贡献,以下说法错误的是( )
| A. | 开普勒通过大量的数据和观测记录,从而发现了行星运行的三大定律 | |
| B. | 卡文迪许利用扭秤实验装置测量出万有引力常量,牛顿在此基础上提出了万有引力定律 | |
| C. | 安培观察到通电螺旋管的磁场和条形磁铁的磁场很相似,提出了分子电流假说 | |
| D. | 伽利略最先把科学实验和数学分析方法相结合,否定了力是维持物体运动状态的原因 |
11. 一半径为R的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}R}{2}$.下列说法中正确的是( )
一半径为R的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}R}{2}$.下列说法中正确的是( )
 一半径为R的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}R}{2}$.下列说法中正确的是( )
一半径为R的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}R}{2}$.下列说法中正确的是( )| A. | 增大入射角α,光线将不再从竖直表面射出 | |
| B. | 不同的单色光有相同的光路产生 | |
| C. | 入射角α无论如何变化,光线都能从竖直表面射出 | |
| D. | 从竖直表面射出光线与竖直方向夹角是30° |
8. 在如图的甲、乙、丙中除导体棒ab可动外,其余部分均固定不动.甲图中的电容器C原来不带电,设导体棒.导轨和直流电源的电阻均可忽略,导体棒和导轨间的摩擦也不计.图中装置均在水平面内,且都处于方向垂直水平面(即纸面)向下的匀强磁场中,导轨足够长,今给导体棒ab 一个向右的初速度v0,导体棒的最终运动状态是( )
在如图的甲、乙、丙中除导体棒ab可动外,其余部分均固定不动.甲图中的电容器C原来不带电,设导体棒.导轨和直流电源的电阻均可忽略,导体棒和导轨间的摩擦也不计.图中装置均在水平面内,且都处于方向垂直水平面(即纸面)向下的匀强磁场中,导轨足够长,今给导体棒ab 一个向右的初速度v0,导体棒的最终运动状态是( )
 在如图的甲、乙、丙中除导体棒ab可动外,其余部分均固定不动.甲图中的电容器C原来不带电,设导体棒.导轨和直流电源的电阻均可忽略,导体棒和导轨间的摩擦也不计.图中装置均在水平面内,且都处于方向垂直水平面(即纸面)向下的匀强磁场中,导轨足够长,今给导体棒ab 一个向右的初速度v0,导体棒的最终运动状态是( )
在如图的甲、乙、丙中除导体棒ab可动外,其余部分均固定不动.甲图中的电容器C原来不带电,设导体棒.导轨和直流电源的电阻均可忽略,导体棒和导轨间的摩擦也不计.图中装置均在水平面内,且都处于方向垂直水平面(即纸面)向下的匀强磁场中,导轨足够长,今给导体棒ab 一个向右的初速度v0,导体棒的最终运动状态是( )| A. | 三种情况下,导体棒ab最终均静止 | |
| B. | 图甲、丙中ab棒最终将以不同的速度做匀速运动;图乙中ab棒最终静止 | |
| C. | 图甲、丙中,ab棒最终将以相同的速度做匀速运动 | |
| D. | 甲乙两种情况下,电阻R上产生的焦耳热一定不同 |
12.在物理学的发展过程中,许多物理学家都做出了重要的贡献,他们也创造出了许多物理学的研究方法,下列关于物理学研究方法的叙述中正确的是( )
| A. | 质点、速度、点电荷等都是理想化模型 | |
| B. | 物理学中所有物理量都是采用比值法定义的 | |
| C. | 牛顿开创了实验研究和逻辑推理相结合探索物理规律的科学方法 | |
| D. | 重心、合力和交变电流的有效值等概念的建立都体现了等效替代的思想 |
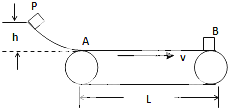 如图所示,质量m=1kg的物体从高为h=0.2m的光滑轨道上P点由静止开始下滑,滑到水平传送带上的A点,物体和皮带之间的动摩擦因数为μ=0.2,传送带AB之间的距离为L=5m,传送带一直以v=4m/s的速度匀速运动,求:
如图所示,质量m=1kg的物体从高为h=0.2m的光滑轨道上P点由静止开始下滑,滑到水平传送带上的A点,物体和皮带之间的动摩擦因数为μ=0.2,传送带AB之间的距离为L=5m,传送带一直以v=4m/s的速度匀速运动,求: 如图所示,理想变压器原线圈的匝数n1=1210,交流电的输出电压U1=220V,电阻R=18Ω,灯泡L上标有“36V 40W”的字样,已知接通电源后灯泡L能正常发光,求副线圈的匝数n2.
如图所示,理想变压器原线圈的匝数n1=1210,交流电的输出电压U1=220V,电阻R=18Ω,灯泡L上标有“36V 40W”的字样,已知接通电源后灯泡L能正常发光,求副线圈的匝数n2.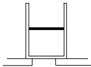 如图所示,汽缸放置在水平平台上,活塞质量为10kg,横截面积为50cm2,厚度为1cm,汽缸全长为21cm,汽缸质量为20kg,大气压强为1×105Pa,当温度为7℃时,活塞封闭的气柱长10cm,若将汽缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2,求:
如图所示,汽缸放置在水平平台上,活塞质量为10kg,横截面积为50cm2,厚度为1cm,汽缸全长为21cm,汽缸质量为20kg,大气压强为1×105Pa,当温度为7℃时,活塞封闭的气柱长10cm,若将汽缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2,求: