题目内容
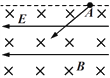
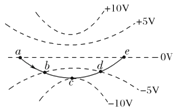
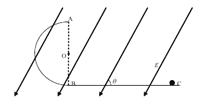
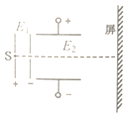
【题目】如图，氕核、氘核、氚核三种粒子从S点无初速释放。经电场
加速后，又进入电场
偏转最后打在屏上。整个装置处于真空中，不计粒子重力及其相互作用，则
A. 三种粒子将打到屏上的不同位置
B. 偏转电场对三种粒子做功一样多
C. 三种粒子打到屏上的动能不同
D. 三种粒子运动到屏上所用时间相同
【答案】B
【解析】
根据动能定理定理可求得粒子刚进入偏转电场时的速度。粒子进入偏转电场中做类平抛运动，由分位移公式得到粒子在偏转电场中的偏转距离，再由几何关系可明确粒子打在屏上的位置。根据电场力做功
可分析偏转电场对粒子做功大小关系，结合动能定理分析粒子打到屏上时速度关系。
粒子在加速电场中加速，由动能定理可知：
，解得：
，粒子在加速电场中的运动时间：
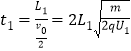；粒子在偏转电场中做类平抛运动，运动时间：
；在偏转电场中竖直分位移：
；联立解得：
，y与q、m无关，所以三种粒子在偏转电场中轨迹重合，离开偏转电场后粒子做匀速直线运动，因此三种粒子一定打到屏上的同一位置；加速电场对粒子做功为
，q和
相等，所以加速电场
对三种粒子做功相等。偏转电场
对粒子做功：
，q、、y相等，则知偏转电场对三种粒子做功相等，故A错误，B正确；对整个过程，根据动能定理得：
，由于W相等，所以三种粒子达到屏上的动能相同，故C错误；离开偏转电场后粒子的运动时间：
；粒子运动到屏上所用时间
；因为
不等，所以t不等，故D错误。所以B正确，ABD错误。
练习册系列答案
相关题目
