题目内容
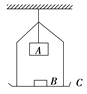
【题目】质量均为M的A、B两个物体由一轻弹簧相连,竖直静置于水平地面上.现有一种方案可以使物体A在被碰撞后的运动过程中,物体B在某一时刻恰好能脱离水平地面.如图所示,质量为m的物块C由距A正上方h处自由下落,与A碰撞后粘合在一起.已知M=2kg,m=1kg,h=0.45m,重力加速度g=10m/s2 , 整个过程弹簧始终处于弹性限度内,不计空气阻力.求: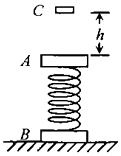
(1)C与A碰撞前瞬间速度的大小;
(2)C、A系统因碰撞损失的机械能;
(3)弹簧的劲度系数k.
【答案】
(1)解:设物体C自由落下h时速度为v,由动能定理得: ![]()
解得: ![]()
(2)解:设物体C与A碰撞并粘合后一起竖直向下运动速度大小为v1,由动量守恒定律得:mv=(m+m)v1
代入数据解得:v1=1m/s
C、A系统因碰撞损失的机械能: ![]()
代入数据得:△E=3J
(3)解:分析C、A共速后的运动过过程,初始时刻弹簧处于压缩状态,设此时的形变量为x,到达最高点时处于拉伸状态,恰好压缩量等于伸长量,取起始位置为重力势能零参考面,由机械能守恒定律得: ![]()
得 ![]()
再由 kx=Mg
解得:k=800N/m
【解析】(1)由机械能守恒定律可以求出C与A碰撞前瞬间速度的大小;(2)由动量守恒定律先求出碰撞后二者共同速度,然后由能量守恒定律可以求出损失的机械能;(3)由平衡条件、动量守恒定律、机械能守恒定律可以求出弹簧的劲度系数k.
【考点精析】利用功能关系和动量守恒定律对题目进行判断即可得到答案,需要熟知当只有重力(或弹簧弹力)做功时,物体的机械能守恒;重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2;合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 (动能定理);除了重力(或弹簧弹力)之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1;动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.