题目内容
1.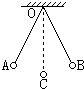 质量为m,带电量为+q的小球用一长度为L的绝缘细线悬于O点,开始时它在A、B之间来回摆动,OA、OB与竖直方向的夹角均为θ,若当小球摆动到B点时突然施加一方向竖直向上、大小E=$\frac{mg}{q}$的匀强电场,则此时线中的拉力大小为0,若这一匀强电场是在小球从A点摆到最低点C时突然加上去的,则当小球运动到B点时线中的拉力大小为2(1-cosθ)mg.
质量为m,带电量为+q的小球用一长度为L的绝缘细线悬于O点,开始时它在A、B之间来回摆动,OA、OB与竖直方向的夹角均为θ,若当小球摆动到B点时突然施加一方向竖直向上、大小E=$\frac{mg}{q}$的匀强电场,则此时线中的拉力大小为0,若这一匀强电场是在小球从A点摆到最低点C时突然加上去的,则当小球运动到B点时线中的拉力大小为2(1-cosθ)mg.
分析 (1)加电场后,电场力与重力平衡,物体保持静止;
(2)加电场后,电场力与重力平衡,物体做匀速圆周运动,拉力提供向心力.
解答 解:(1)电场力F=qE=mg,故电场力与重力平衡;运动到最高点加电场,小球由于惯性保持静止,故细线的拉力为零;
(2)如果这一电场是在小球从A点摆到最低点C时突然加上去的,由于重力与电场力平衡,故此后小球做匀速圆周运动,拉力提供向心力,根据牛顿第二定律,有:
T2=m$\frac{{v}^{2}}{L}$
从A到C过程,根据动能定理,有:
mgL(1-cosθ)=$\frac{1}{2}m{v}^{2}$
联立解得:
T2=2(1-cosθ)mg
故答案为:0;2(1-cosθ)mg.
点评 本题关键是明确小球的运动情况和受力情况,由于电场力和重力平衡,故加电场力相当于突然撤去重力,基础问题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
12.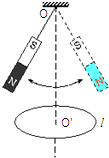 如图,一条形磁铁用线悬挂于0点,在O点的正下方固定放置一水平的金属圆环l.现使磁铁沿竖直平面来回摆动,则( )
如图,一条形磁铁用线悬挂于0点,在O点的正下方固定放置一水平的金属圆环l.现使磁铁沿竖直平面来回摆动,则( )
 如图,一条形磁铁用线悬挂于0点,在O点的正下方固定放置一水平的金属圆环l.现使磁铁沿竖直平面来回摆动,则( )
如图,一条形磁铁用线悬挂于0点,在O点的正下方固定放置一水平的金属圆环l.现使磁铁沿竖直平面来回摆动,则( )| A. | 在一个周期内,圆环中感应电流方向改变二次 | |
| B. | 磁铁始终受到感应电流磁场的斥力作用 | |
| C. | 磁铁所受感应电流磁场的作用力有时是阻力,有时是动力 | |
| D. | 磁铁所受感应电流磁场的作用力始终是阻力 |
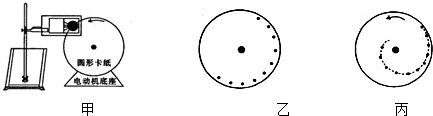
9.正弦交流电的电流图象如图所示,则( )


| A. | 电流的有效值是0.05A | |
| B. | 电流的频率是100HZ | |
| C. | t=0.01s线圈与中性面重合 | |
| D. | 电流的函数表达式i=0.05sin(100πt)A |
6.关于磁场的说法中,不正确的是( )
| A. | 磁场中某点的磁场方向与放在该点的小磁针所受磁场力的方向相同 | |
| B. | 磁场中某点的磁场方向与通过该点的磁感线的切线方向相同 | |
| C. | 磁场对运动的电荷不一定有力的作用 | |
| D. | 描述磁场分布的磁感线一定是闭合的 |
13.对超导现象的研究是当今科技的热点.当一块磁体靠近超导体时,超导体会产生强大的电流,对磁体产生排斥作用.这种排斥力可使磁体悬浮在空中.磁悬浮列车就是采用了这种技术.磁体悬浮的原理是( )
| A. | 超导体电流的磁场方向与磁体磁场方向相同 | |
| B. | 超导体电流的磁场方向与磁体磁场方向相反 | |
| C. | 超导体使磁体处于失重状态 | |
| D. | 超导体产生的磁力和磁体的重力是一对作用力与反作用力 |
10.下列说法中正确的是( )
| A. | 只要有电荷存在,电荷周围就一定存在着电场 | |
| B. | 电场是一种物质,与其他物质一样,是不依赖我们的感觉而客观存在的东西 | |
| C. | 电场可以用电场线来描述,电场线是电场中客观存在的一簇曲线 | |
| D. | 电场是人为设想出来的.其实并不存在 |
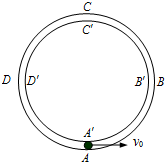 如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD的光滑,内圆A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑,一质量m=2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,球运动的半径R=0.2m,取g=10m/s2.
如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD的光滑,内圆A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑,一质量m=2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,球运动的半径R=0.2m,取g=10m/s2. 如图所示,一质量为m的物体压在置于水平面上的劲度系数为k的竖直轻弹簧上,用一根弹性细绳跨过定滑轮与物体连接,弹性细绳伸直且没有位力时,其端点位于M位置,慢慢拉细绳直到端点到N位置时,弹簧对物体的拉力大小恰好等于物体的重力.已知这种细绳的弹力与伸长量成正比,比例系数为k′.求:
如图所示,一质量为m的物体压在置于水平面上的劲度系数为k的竖直轻弹簧上,用一根弹性细绳跨过定滑轮与物体连接,弹性细绳伸直且没有位力时,其端点位于M位置,慢慢拉细绳直到端点到N位置时,弹簧对物体的拉力大小恰好等于物体的重力.已知这种细绳的弹力与伸长量成正比,比例系数为k′.求: