题目内容
(12分)如图所示，跳台滑雪运动中，运动员经过一段加速滑行后从O点水平飞出，经过t＝3.0s落到斜坡上的A点，已知O点是斜坡的起点，斜坡与水平面的夹角为θ＝37°，运动员的质量为m＝50kg，不计空气阻力，取sin37°＝0.6，cos37°＝0.8，g＝10m/s2，求：
⑴A点与O点间的距离L；
⑵运动员离开O点时的速率v0；
⑶运动员落到A点时的速度v。
⑴A点与O点间的距离L；
⑵运动员离开O点时的速率v0；
⑶运动员落到A点时的速度v。
⑴L＝75m；⑵v0＝20m/s；⑶v＝
m/s，方向与水平方向的夹角为：α＝arctanα
m/s，方向与水平方向的夹角为：α＝arctanα试题分析：⑴运动员从O点水平飞出后，做平抛运动至A点，在竖直方向上，根据自由落体运动规律可知，运动员下落的高度为：h＝
①根据图中几何关系可知：L＝
②由①②式联立解得A点与O点间的距离为：L＝
＝75m⑵A点与O点间的水平距离为：x＝
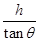③在水平方向上运动员做匀速运动，所以有：v0＝
④由①③④式联立解得运动员离开O点时的速率为：v0＝
＝20m/s⑶在竖直方向上vy＝gt＝30m/s
所以运动员落到A点时的速度大小为：v＝
＝m/s设其方向与水平方向的夹角为α，则：tanα＝
＝，即α＝arctan
练习册系列答案
相关题目
发射一颗炮弹欲轰炸地面目标P，反应灵敏的地面拦截系统同时以速度
竖直向上发射炮弹拦截. 设拦截系统与飞机的水平距离为s，若拦截成功，不计空气阻力，则
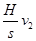
v0，不计空气阻力，重力加速度为g，以下说法正确的是（ ）
v0
.
