题目内容
16. 在“探究小车速度随时间均匀变化的规律”的声音中,得到一条纸带如图所示,A、B、C、D、E、F为相邻的6个计数点,若相邻计数点的时间间隔为t=0.1s,量的AB=1.5cm、EF=3.1cm,可估测小车的加速度大小为040m/s2,由此可进一步求出打下B点时小车的速度大小0.17为m/s.
在“探究小车速度随时间均匀变化的规律”的声音中,得到一条纸带如图所示,A、B、C、D、E、F为相邻的6个计数点,若相邻计数点的时间间隔为t=0.1s,量的AB=1.5cm、EF=3.1cm,可估测小车的加速度大小为040m/s2,由此可进一步求出打下B点时小车的速度大小0.17为m/s.
分析 根据连续相等时间内的位移之差是一恒量求出加速度,以及BC间的距离,根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的速度大小.
解答 解:根据${x}_{EF}-{x}_{AB}=4a{T}^{2}$得,加速度a=$\frac{{x}_{EF}-{x}_{AB}}{4{T}^{2}}=\frac{(3.1-1.5)×1{0}^{-2}}{4×0.01}$m/s2=0.40m/s2.
BC间的距离${x}_{BC}={x}_{AB}+a{T}^{2}=0.015+0.4×0.01$m=1.9cm.
则B点的瞬时速度${v}_{B}=\frac{{x}_{AB}+{x}_{BC}}{2T}=\frac{(1.5+1.9)×1{0}^{-2}}{0.2}$m/s=0.17m/s.
故答案为:0.40,0.17.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.

练习册系列答案
相关题目
7.质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位),则该质点( )
| A. | 第1s内的位移是5m | B. | 前2s内的平均速度是7m/s | ||
| C. | 任意相邻的1s 内位移差都是1m | D. | 任意1s内的速度增量都是4m/s |
7.在x轴上A、B两处分别放有两个点电荷,A处为-Q,B处为+2Q,在x轴上某处,两个电荷各自产生电场强度数值为EA和EB,则( )
| A. | EA=EB之点,只有一处,该处合场强为0 | |
| B. | EA=EB之点有两处,一处合场强为0,另一处合场强为2EA | |
| C. | EA=EB之点共有三处,其中两处合场强为0;另一处合场强为2EA | |
| D. | EA=EB之点共有三处,其中一处合场强为0,另二处合场强为2EA |
4. 如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )
如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )
 如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )
如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )| A. | ab所在电场线方向为竖直向上 | |
| B. | 带电粒子从a点运动到b点过程中电场力做功为零 | |
| C. | a、b两点间的电势差Uab=-$\frac{mgh}{q}$ | |
| D. | b点场强大于a点场强 |
1.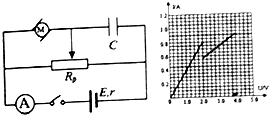 如左图,电源电动势Er内阻r,电动机M伏安特性曲线如图,闭合开关,电动机处于运转状态,若滑动变阻器的滑动触头向右移动一些,以下说法正确的是( )
如左图,电源电动势Er内阻r,电动机M伏安特性曲线如图,闭合开关,电动机处于运转状态,若滑动变阻器的滑动触头向右移动一些,以下说法正确的是( )
 如左图,电源电动势Er内阻r,电动机M伏安特性曲线如图,闭合开关,电动机处于运转状态,若滑动变阻器的滑动触头向右移动一些,以下说法正确的是( )
如左图,电源电动势Er内阻r,电动机M伏安特性曲线如图,闭合开关,电动机处于运转状态,若滑动变阻器的滑动触头向右移动一些,以下说法正确的是( )| A. | 电容器C的带电量增加 | B. | 电动机产热功率增大 | ||
| C. | 电流表示数增大 | D. | 路端电压减小 |
8.做匀加速直线运动的物体在时间T 内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则以下判断正确的有( )
| A. | 物体经A点的速度大小为$\frac{{x}_{1}+{x}_{2}}{2T}$ | |
| B. | 物体运动的加速度为$\frac{{x}_{1}+{x}_{2}}{{T}^{2}}$ | |
| C. | 物体到达B点的速度大小为 $\frac{{x}_{1}+{x}_{2}}{T}$ | |
| D. | 物体运动的加速度为$\frac{{x}_{2}-{x}_{1}}{{T}^{2}}$ |
5.如图所示,一根弹性细绳原长为l,劲度系数为k,将其一端穿过一个光滑小孔O(其在水平地面上的投影点为O′),系在一个质量为m的滑块A上,A放在水平地面上.小孔O离绳固定端的竖直距离为l,离水平地面高度为h(h<$\frac{mg}{k}$),滑块A与水平地面间的最大静摩擦力为压力的μ倍,用一水平外力将滑块A从O′点缓慢拉到与O′点距离为r时,撤掉外力滑块A恰好能保持静止状态,则( )
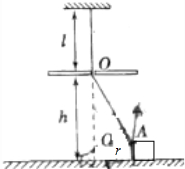

| A. | 当滑块与O′点距离为r时,弹性绳的拉力F=k$\sqrt{{h}^{2}+{r}^{2}}$ | |
| B. | 在滑块A向右缓慢运动的过程中,地面对滑块的支持力逐渐增大 | |
| C. | 在滑块A向右缓慢运动的过程中,地面对滑块的摩擦力逐渐减小 | |
| D. | 滑块可以在以O′为圆心,以$\frac{μ(mg-kh)}{k}$为半径的水平地面上的圆内的任何位置保持静止状态 |
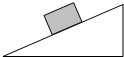 如图所示,一个重为5N的物体静止在倾斜角为30°的粗糙斜面上,该物体受到沿斜面向上的3N的摩擦力和4N的支持力,则:
如图所示,一个重为5N的物体静止在倾斜角为30°的粗糙斜面上,该物体受到沿斜面向上的3N的摩擦力和4N的支持力,则: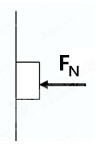 如图所示,用水平力FN将质量为m=1kg的物体压在竖直墙壁上,已知物体与墙壁之间的动摩擦因数μ=0.2,取g=10N/kg.
如图所示,用水平力FN将质量为m=1kg的物体压在竖直墙壁上,已知物体与墙壁之间的动摩擦因数μ=0.2,取g=10N/kg.