题目内容
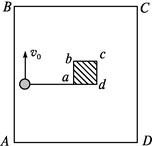
(15分)如图所示,在光滑水平桌面ABCD中央固定一边长为0.4 m的光滑小方柱abcd.长为L=1 m的细线,一端拴在a上,另一端拴住一个质量为m=0.5 kg的小球.小球的初始位置在ad连线上a的一侧,且把细线拉直,并给小球以v0=2 m/s的垂直于细线方向的水平速度使它做圆周运动.由于光滑小方柱abcd的存在,使线逐步缠在abcd上.若细线能承受的最大张力为7 N(即线所受的拉力大于或等于7 N时立即断裂),那么从开始运动到细线断裂经过的时间为多少?小球从桌面的哪一边飞离桌面?

1.256 s 从AD边飞离桌面
设当线长为L0时,线将断裂.根据向心力公式得T=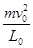 ,所以L0=0.29 m.
,所以L0=0.29 m.
绕a点转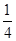 周的时间
周的时间
t1=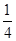 ×
× =0.785 s,
=0.785 s,
绕b点转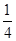 周的时间
周的时间
t2=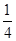 ×
×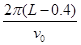 =0.471 s,
=0.471 s,
线接触c点后,小球做圆周运动的半径为r=0.2 m,小于L0=0.29 m,所以线立即断裂.
所以从开始运动到线断裂经过t=1.256 s,小球从桌面的AD边飞离桌面.
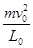 ,所以L0=0.29 m.
,所以L0=0.29 m.绕a点转
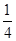 周的时间
周的时间t1=
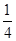 ×
× =0.785 s,
=0.785 s,绕b点转
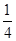 周的时间
周的时间t2=
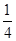 ×
×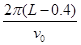 =0.471 s,
=0.471 s,线接触c点后,小球做圆周运动的半径为r=0.2 m,小于L0=0.29 m,所以线立即断裂.
所以从开始运动到线断裂经过t=1.256 s,小球从桌面的AD边飞离桌面.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

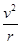 ,所以a与v2成正比
,所以a与v2成正比
 小于
小于