题目内容
(1)如图甲所示,在杨氏双缝干涉实验中,激光的波长为5.30×10-7m,屏上P点距双缝
和
的路程差7.95×10-7m.则在这里出现的应是

(2)如图乙所示,一束激光从O点由空气射入厚度均匀的介质,经下表面反射后,从上面的A点射出.已知入射角为i,A与O 相距L,介质的折射率为n,试求介质的厚度d.
| s | 1 |
| s | 2 |
暗条纹
暗条纹
(选填“明条纹”或“暗条纹”).现改用波长为6.30×10-7m的激光进行上述实验,保持其他条件不变,则屏上的条纹间距将变宽
变宽
(填“变宽”、“变窄”、或“不变”.
(2)如图乙所示,一束激光从O点由空气射入厚度均匀的介质,经下表面反射后,从上面的A点射出.已知入射角为i,A与O 相距L,介质的折射率为n,试求介质的厚度d.
分析:(1)当光屏上的点到双缝的路程差是半波长的偶数倍,出现明条纹;路程差是半波长的奇数倍,出现暗条纹.根据△x=
λ判断条纹间距的变化.
(2)已知入射角i和折射率n,根据折射定律求出光在介质上界面的折射角r,由几何关系求出介质的厚度d.
| L |
| d |
(2)已知入射角i和折射率n,根据折射定律求出光在介质上界面的折射角r,由几何关系求出介质的厚度d.
解答:解:屏上P点距双缝s1和s2的路程差为7.95×10-7m,则:
n=
=
=3,3为奇数,在P点出现暗条纹.
根据△x=
λ知,波长变大,则条纹间距变宽.
(2)由
=n得:
sinr=
①
由几何关系得:介质的厚度:
d=
cotγ=
?
r ②
由①②解得:
d=
.
故答案为:(1)暗条纹;变宽.(2)介质的厚度d=
.
n=
| △s | ||
|
| 7.95×10-7m | ||
|
根据△x=
| L |
| d |
(2)由
| sini |
| sinγ |
sinr=
| sini |
| n |
由几何关系得:介质的厚度:
d=
| L |
| 2 |
| L |
| 2 |
| cosγ |
| sinγ |
由①②解得:
d=
| L |
| 2 |
|
故答案为:(1)暗条纹;变宽.(2)介质的厚度d=
| L |
| 2 |
|
点评:本题第一问关键关键掌握出现明暗条纹的条件,以及掌握双缝干涉条纹的间距公式△x=
λ;第二问是折射定律与几何知识的综合应用,抓住入射角、折射角、折射率等各个量的关系研究是解题的基础.
| L |
| d |

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目



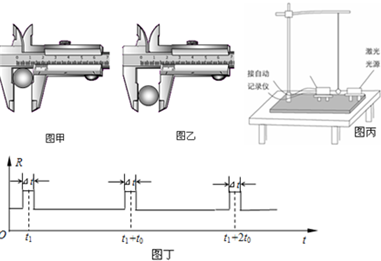 (2)实验时,若摆球在垂直纸面的平面内摆动,为了将人工记录振动次数改为自动记录振动次数,在摆球运动最低点的左、右两侧分别放置一激光光源与光敏电阻,如图甲所示.光敏电阻与某一自动记录相连,该仪器显示的光敏电阻阻值R随时间t变化图线如图乙所示,则该单摆的振动周期为
(2)实验时,若摆球在垂直纸面的平面内摆动,为了将人工记录振动次数改为自动记录振动次数,在摆球运动最低点的左、右两侧分别放置一激光光源与光敏电阻,如图甲所示.光敏电阻与某一自动记录相连,该仪器显示的光敏电阻阻值R随时间t变化图线如图乙所示,则该单摆的振动周期为