题目内容
根据单摆周期公式T=2π
,可以通过实验测量当地的重力加速度.如图1所示,将细线的上端固定在铁架台上,下端系一小钢球,就做成了单摆.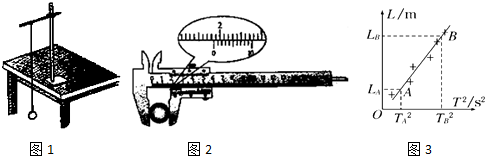
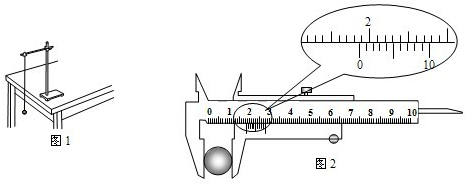
(1)用游标卡尺测量小钢球直径,求数如图2所示,读数为 mm.
(2)以下是实验过程中的一些做法,其中正确的有 .
a.摆线要选择细些的、伸缩性小些的,并且尽可能长一些
b.摆球尽量选择质量大些、体积小些的
c.为了使摆的周期大一些,以方便测量,开始时拉开摆球,使摆线相距平衡位置有较大的角度
d.拉开摆球,使摆线偏离平衡位置大于5°,在释放摆球的同时开始计时,当摆球回到开始位置时停止计时,此时间间隔△t即为单摆周期T
e.拉开摆球,使摆线偏离平衡位置不大于5°,释放摆球,当摆球振动稳定后,从平衡位置开始计时,记下摆球做50次全振动所用的时间△t,则单摆周期T=△t/50
(3)若该实验单摆静止时摆球重心在球心的正下方,仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两个点,坐标如图3所示.采用恰当的数据处理方法也能正确的求出当地的重力加速度,则计算重力加速度的表达式应为g= .
|

(1)用游标卡尺测量小钢球直径,求数如图2所示,读数为
(2)以下是实验过程中的一些做法,其中正确的有
a.摆线要选择细些的、伸缩性小些的,并且尽可能长一些
b.摆球尽量选择质量大些、体积小些的
c.为了使摆的周期大一些,以方便测量,开始时拉开摆球,使摆线相距平衡位置有较大的角度
d.拉开摆球,使摆线偏离平衡位置大于5°,在释放摆球的同时开始计时,当摆球回到开始位置时停止计时,此时间间隔△t即为单摆周期T
e.拉开摆球,使摆线偏离平衡位置不大于5°,释放摆球,当摆球振动稳定后,从平衡位置开始计时,记下摆球做50次全振动所用的时间△t,则单摆周期T=△t/50
(3)若该实验单摆静止时摆球重心在球心的正下方,仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两个点,坐标如图3所示.采用恰当的数据处理方法也能正确的求出当地的重力加速度,则计算重力加速度的表达式应为g=
分析:(1)游标卡尺的读数方法是先读出主尺上的刻度,再看游标尺上的哪一刻度与固定的刻度对齐;
(2)摆线要选择细些的、伸缩性小些的;摆球尽量选择质量大些、体积小些的摆球振动稳定后,从平衡位置开始计时;摆线偏离平衡位置不大于5°;
(3)由单摆周期公式的变形公式求出L-T2关系表达式,然后根据图象求出重力加速度.
(2)摆线要选择细些的、伸缩性小些的;摆球尽量选择质量大些、体积小些的摆球振动稳定后,从平衡位置开始计时;摆线偏离平衡位置不大于5°;
(3)由单摆周期公式的变形公式求出L-T2关系表达式,然后根据图象求出重力加速度.
解答:解:(1)游标卡尺的读数方法是先读出主尺上的刻度,大小:18mm,再看游标尺上的哪一刻度与固定的刻度对齐:第6刻度与上方刻度对齐,读数:0.1×6=0.6mm,总读数:L=18+0.6=18.6mm.
(2)该实验中,要选择细些的、伸缩性小些的摆线,长度要适当长一些;和选择体积比较小,密度较大的小球.故ab是正确的.
摆球的周期与摆线的长短有关,与摆角无关,故c错误;
拉开摆球,使摆线偏离平衡位置不大于5°,故d错误;释放摆球,当摆球振动稳定后,从平衡位置开始计时;要测量多个周期的时间,然后求平均值.故e正确.故选择:abe.
(3)由单摆周期公式T=2π
可知,l=
T2,故L-T2图线的斜率为:
;
由L-T2图线得到:
=
故:
=
解得:g=
故答案为:
(1)18.6;
(2)abe;
(3)
.
(2)该实验中,要选择细些的、伸缩性小些的摆线,长度要适当长一些;和选择体积比较小,密度较大的小球.故ab是正确的.
摆球的周期与摆线的长短有关,与摆角无关,故c错误;
拉开摆球,使摆线偏离平衡位置不大于5°,故d错误;释放摆球,当摆球振动稳定后,从平衡位置开始计时;要测量多个周期的时间,然后求平均值.故e正确.故选择:abe.
(3)由单摆周期公式T=2π
|
| g |
| 4π2 |
| g |
| 4π2 |
由L-T2图线得到:
| △L |
| △(T2) |
| LB-LA | ||||
|
故:
| g |
| 4π2 |
| LB-LA | ||||
|
解得:g=
| 4π2(LB-LA) | ||||
|
故答案为:
(1)18.6;
(2)abe;
(3)
| 4π2(LB-LA) | ||||
|
点评:该题前二问考查游标卡尺的读数方法与用单摆测量重力加速度实验中的几个注意事项,要求对该部分知识有准确的记忆;第三问关键是由单摆周期公式求出l与T2的关系式进行分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,是一个内表面光滑圆桶的一部分,其半径很大,为了检测圆桶内部的直径D大小,请你利用如下器材设计一个实验.现提供器材如下:
如图所示,是一个内表面光滑圆桶的一部分,其半径很大,为了检测圆桶内部的直径D大小,请你利用如下器材设计一个实验.现提供器材如下: (1)某同学在“用单摆测定重力加速度”的实验中,通过测量单摆摆长L,利用秒表记录该单摆50次全振动所用的时间并求出周期T,根据单摆周期公式T=2π
(1)某同学在“用单摆测定重力加速度”的实验中,通过测量单摆摆长L,利用秒表记录该单摆50次全振动所用的时间并求出周期T,根据单摆周期公式T=2π