题目内容
6.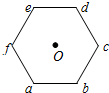 边长为L的正六边形abcdef的顶点a上固定一个电量为2Q的正点电荷,其余各顶点固定一个电量均为Q的负点电荷,则O点的电场强度为( )
边长为L的正六边形abcdef的顶点a上固定一个电量为2Q的正点电荷,其余各顶点固定一个电量均为Q的负点电荷,则O点的电场强度为( )| A. | $\frac{2kQ}{L^2}$,方向O→d | B. | $\frac{3kQ}{L^2}$,方向O→d | C. | $\frac{2kQ}{L^2}$,方向d→O | D. | $\frac{3kQ}{L^2}$,方向d→O |
分析 根据电场的叠加原理和对称性,确定O点的场强大小,并分析出电场强度的方向.
解答 解:a处电量+2Q的正电荷在O处产生的场强大小为 E1=k$\frac{2Q}{{L}^{2}}$,方向O→d,
d处的-Q在O点处产生的场强大小为 E2=k$\frac{Q}{{L}^{2}}$,方向O→d.由于b处与e处负电荷在O点处产生的场强大小相等、方向相反,相互抵消;c处与f处负电荷在O点处产生的场强大小相等、方向相反,相互抵消;所以根据电场的叠加原理可知O处的场强等于a处和d处两个电荷产生的电场的叠加,因此O点的电场强度大小为 E=E1+E2=$\frac{3kQ}{{L}^{2}}$,方向O→d.
故选:B
点评 本题要知道点电荷的电场的分布,掌握点电荷场强公式,充分利用对称性,由电场的叠加原理来解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下列说法中正确的是( )
| A. | 匀强电场中各处场强相等,电势也相等 | |
| B. | 等势体内各点电势相等.场强为零 | |
| C. | 沿电场线方向电场强度一定越来越小 |
17. 如图所示,光滑轨道LMNPQMK固定在水平地面上,轨道平面在竖直面内,MNPQM是半径为R的圆形轨道,轨道LM与圆形轨道MNPQM在M点相切,轨道MK与圆形轨道MNPQM在M点相切,b点、P点在同一水平面上,K点位置比P点低,b点离地高度为2R,a点离地高度为2.5R,若将一个质量为m的小球从左侧轨道上不同位置由静止释放,关于小球的运动情况,以下说法中正确的是( )
如图所示,光滑轨道LMNPQMK固定在水平地面上,轨道平面在竖直面内,MNPQM是半径为R的圆形轨道,轨道LM与圆形轨道MNPQM在M点相切,轨道MK与圆形轨道MNPQM在M点相切,b点、P点在同一水平面上,K点位置比P点低,b点离地高度为2R,a点离地高度为2.5R,若将一个质量为m的小球从左侧轨道上不同位置由静止释放,关于小球的运动情况,以下说法中正确的是( )
 如图所示,光滑轨道LMNPQMK固定在水平地面上,轨道平面在竖直面内,MNPQM是半径为R的圆形轨道,轨道LM与圆形轨道MNPQM在M点相切,轨道MK与圆形轨道MNPQM在M点相切,b点、P点在同一水平面上,K点位置比P点低,b点离地高度为2R,a点离地高度为2.5R,若将一个质量为m的小球从左侧轨道上不同位置由静止释放,关于小球的运动情况,以下说法中正确的是( )
如图所示,光滑轨道LMNPQMK固定在水平地面上,轨道平面在竖直面内,MNPQM是半径为R的圆形轨道,轨道LM与圆形轨道MNPQM在M点相切,轨道MK与圆形轨道MNPQM在M点相切,b点、P点在同一水平面上,K点位置比P点低,b点离地高度为2R,a点离地高度为2.5R,若将一个质量为m的小球从左侧轨道上不同位置由静止释放,关于小球的运动情况,以下说法中正确的是( )| A. | 若将小球从LM轨道上a由静止释放,小球一定不能沿轨道运动到K点 | |
| B. | 若将小球从LM轨道上b点由静止释放,小球一定不能沿轨道运动到K点 | |
| C. | 若将小球从LM轨道上a、b点之间任一位置由静止释放,小球一定能沿轨道运动到K点 | |
| D. | 若将小球从LM轨道上a点以上任一位置由静止释放,小球沿轨道运动到K点后做斜上抛运动,小球做斜上抛运动时距离地面的最大高度一定小于由静止释放时的高度 |
14.酒后驾驶会导致许多安全隐患,是因为驾驶员的反应时间变长.反应时间是指驾驶员从发现情况到采取制动的时间.如表中“思考距离”是指驾驶员发现情况到采取制动的时间内汽车行驶的距离;“制动距离”是指驾驶员发现情况到汽车停止行驶的距离(假设汽车制动时的加速度大小都相同).分析表中信息求:
(1)汽车制动后减速的加速度大小
(2)若酒后驾驶汽车以25m/s的加速度行驶时,发现前方60m处有险情,问能不能安全停车.
| 速度(m/s) | 思考距离/m | 制动距离/m | ||
| 正常x1 | 酒后x2 | 正常x3 | 酒后x4 | |
| 15 | 7.5 | 15.0 | 22.5 | 30.0 |
| 20 | 10.0 | 20.0 | 36.7 | 46.7 |
(2)若酒后驾驶汽车以25m/s的加速度行驶时,发现前方60m处有险情,问能不能安全停车.
11. 如图所示,在足够大的粗糙水平绝缘面上固定着一个点电荷Q,将一个质量为m 的带电物块q(可视为质点)在水平面上由静止释放,物块将在水平面上沿远离Q 的方向开始运动.则在物块从开始运动到停下的整个过程中( )
如图所示,在足够大的粗糙水平绝缘面上固定着一个点电荷Q,将一个质量为m 的带电物块q(可视为质点)在水平面上由静止释放,物块将在水平面上沿远离Q 的方向开始运动.则在物块从开始运动到停下的整个过程中( )
 如图所示,在足够大的粗糙水平绝缘面上固定着一个点电荷Q,将一个质量为m 的带电物块q(可视为质点)在水平面上由静止释放,物块将在水平面上沿远离Q 的方向开始运动.则在物块从开始运动到停下的整个过程中( )
如图所示,在足够大的粗糙水平绝缘面上固定着一个点电荷Q,将一个质量为m 的带电物块q(可视为质点)在水平面上由静止释放,物块将在水平面上沿远离Q 的方向开始运动.则在物块从开始运动到停下的整个过程中( )| A. | 物块的加速度一直变大 | |
| B. | 物块的电势能一直减小 | |
| C. | 电场力对物块做功的数值等于物块增加的机械能 | |
| D. | 电场力对物块做功的数值等于系统摩擦产生的热 |
15. 如图所示,水平光滑长杆上套有小物块A,细线跨过位于O点的轻小定滑轮,一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为O点正下方杆上的点,滑轮到杆距离OC=h.开始时A位于P点,PO与水平方向的夹角为30°.现将A、B由静止释放,则下列说法正确的是( )
如图所示,水平光滑长杆上套有小物块A,细线跨过位于O点的轻小定滑轮,一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为O点正下方杆上的点,滑轮到杆距离OC=h.开始时A位于P点,PO与水平方向的夹角为30°.现将A、B由静止释放,则下列说法正确的是( )
 如图所示,水平光滑长杆上套有小物块A,细线跨过位于O点的轻小定滑轮,一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为O点正下方杆上的点,滑轮到杆距离OC=h.开始时A位于P点,PO与水平方向的夹角为30°.现将A、B由静止释放,则下列说法正确的是( )
如图所示,水平光滑长杆上套有小物块A,细线跨过位于O点的轻小定滑轮,一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为O点正下方杆上的点,滑轮到杆距离OC=h.开始时A位于P点,PO与水平方向的夹角为30°.现将A、B由静止释放,则下列说法正确的是( )| A. | 物块A由P点出发第一次到达C点过程中,速度不断增大 | |
| B. | 在物块A由P点出发第一次到达C点过程中,物块B克服细线拉力做的功小于B重力势能的减少量 | |
| C. | 物块A的速度始终大于物块B的速度 | |
| D. | 物块A经过C点时的速度大小为$\sqrt{2gh}$ |
16.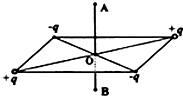 如图所示,将等量的正、负电荷分别放在正方形的四个顶点上.O点为该正方形对角线的交点,直线段AB通过O点且垂直于该正方形,以下对A、B两点的电势和场强的判断,正确的是( )
如图所示,将等量的正、负电荷分别放在正方形的四个顶点上.O点为该正方形对角线的交点,直线段AB通过O点且垂直于该正方形,以下对A、B两点的电势和场强的判断,正确的是( )
 如图所示,将等量的正、负电荷分别放在正方形的四个顶点上.O点为该正方形对角线的交点,直线段AB通过O点且垂直于该正方形,以下对A、B两点的电势和场强的判断,正确的是( )
如图所示,将等量的正、负电荷分别放在正方形的四个顶点上.O点为该正方形对角线的交点,直线段AB通过O点且垂直于该正方形,以下对A、B两点的电势和场强的判断,正确的是( )| A. | EA=EB=0,φA=φB=0 | B. | EA=EB≠0,φA=φB=0 | C. | EA=EB=0,φA=φB≠0 | D. | EA=EB≠0,φA=φB≠0 |

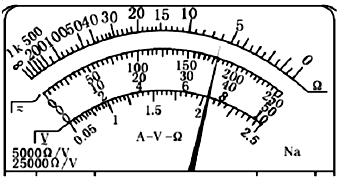 (1)一多用电表的欧姆挡有三个倍率,分别是“×1”、“×10”、“×100”.用“×10”挡测量某电阻时,操作步骤正确,而表头指针偏转角度很小,为了较准确地进行测量,应换用“×100”挡.若将该表选择旋钮置于25mA挡,表盘的示数如下图所示,则被测电流为18.0 mA.
(1)一多用电表的欧姆挡有三个倍率,分别是“×1”、“×10”、“×100”.用“×10”挡测量某电阻时,操作步骤正确,而表头指针偏转角度很小,为了较准确地进行测量,应换用“×100”挡.若将该表选择旋钮置于25mA挡,表盘的示数如下图所示,则被测电流为18.0 mA.