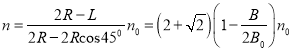题目内容
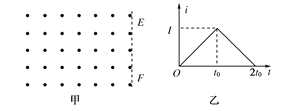
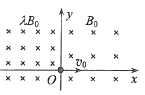
【题目】如图所示,x轴上方存在垂直纸面向外的匀强磁场,坐标原点处有一正离子源,单位时间在xOy平面内发射n0个速率为v的离子,分布在y轴两侧各为θ的范围内.在x轴上放置长度为L的离子收集板,其右端点距坐标原点的距离为2L,当磁感应强度为B0时,沿y轴正方向入射的离子,恰好打在收集板的右端点.不计重力,不考虑离子间的碰撞和相互作用,不计离子在磁场中运动的时间.
(1) 求离子的比荷![]() ;
;
(2) 当磁感应强度为B0时,若发射的离子能被收集板全部收集,求θ须满足的条件;
(3) 若θ=45°,且假设离子到达x轴上时沿x轴均匀分布.
①为使离子不能被收集板所收集,求磁感应强度B应满足的条件(用B0表示);
②若磁感应强度B的取值范围为B0≤B≤2B0,求单位时间内收集板收集到的离子数n与B之间的关系(用B0、n0表示).
【答案】(1) ![]() (2)
(2)![]() (3)
(3) 
【解析】(1) 洛伦兹力提供向心力qvB0=m![]()
圆周运动的半径R=L
解得![]()
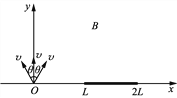
(2) 如图1所示,当以最大角θm入射时,有2Rcosθm=L
解得θm=![]()
发射的离子能被收集板全部收集,θ<![]() .
.
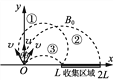
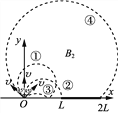
图1 图2
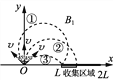
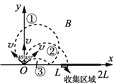
图3 图4
(3) 当θ=45°时
①设收集板恰好收集不到离子时的半径R1,对应的磁感应强度为B1,如图2中①②③所示有2R1=L
对应的磁感应强度B1=2B0
另一种情况:粒子的半径为R′1,对应的磁感应强度为B′1,如若图2中④所示Rcos45°=L
对应的磁感应强度B′1=![]() B0
B0
磁感应强度应满足B>2B0或B′1<![]() B0
B0
②设收集板能全部收集到离子时的最小半径为R2,对应的磁感应强度为B2,如图3所示有2R2cos45°=L
对应的磁感应强度B2=![]() =
=![]() B0
B0
当B0≤B≤![]() B0时,单位时间内收集板收集到的离子数n=n0
B0时,单位时间内收集板收集到的离子数n=n0
当![]() B0<B≤2B0时,如图4所示,单位时间内收集板收集到的离子数为n,则:
B0<B≤2B0时,如图4所示,单位时间内收集板收集到的离子数为n,则: