Question

【题目】如图所示，光滑水平面上有一静止长木板C，其右端带有挡板，小物块A、B分别静置于其左端及中点。已知木板C全长L=18m，物块A、B与木板C间的动摩擦因数皆为μ=0.3，三者质量满足mC=2mA=2mB，重力加速度g=10m/s2.现通过击打使得A物块获得向右的速度v0=15m/s，如果物体间的碰撞都是弹性正碰，试求：

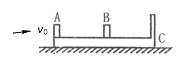
(1)物块A、B第一次碰撞前的速度大小各为多少？

(2)B物块与木板C右端挡板碰后瞬间的速度；

(3)若物块A、B第二次相碰于木板C左端，则v0应为多大？

Answer 1

【答案】(1) , (2) ，故B与C碰后速度为1.5m/s向左 (3)

【解析】(1)设，则，另向右为正方向，刚开始A加速度大小

BC共同的加速度大小

此时BC可保持共速，设A、B第一次相撞时时间为t，则：

解得

所以碰撞前A的速度

碰撞前B的速度

其它合理、正确解法也可得分。

(2)A、B是弹性碰撞且质量相等，则碰撞后速度交换，因此碰后A相对C静止以加速，B延续碰前A的速度以减速。

设B与C右端挡板碰前，B的速度为，AC的速度为，从开始运动至此时刻，由动量守恒和能量关系：

解得： ， (舍)

设B与C右端碰撞后速度分别为、，由动量守恒及机械能守恒

解得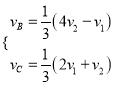， (舍)

代入数据得，故B与C碰后速度为1.5m/s向左

其它合理、正确解法也可得分。

(3)碰后A、B、C速度分别为、、，且有，因此碰后A、B都相对C向左滑，A、B加速度大小为，而C加速度大小为

BC碰后，因为AC间相对速度比BC间小，所以AC间先达到相对静止，假设此过程AB并未相撞且未掉下木板，设所经历时间为t，有，得：

此过程A相对C位移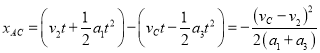

此过程A、B无相对加速度，因此相对做匀速运动，B相对A位移为

可得，代入可得。

因题目要求AB相碰时的相对位移m，所以此时即A、C正好相对速度为0时A、B正好相撞，由题意相撞位置正好在C左端，故m，代入可得

m/sm/s

可解得m/s