题目内容
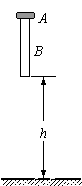
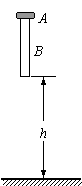
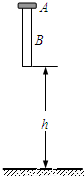
如图所示,一圆环A套在一粗细均匀的圆木棒B上,圆环A的高度相对B的长度可以忽略不计.A和B的质量都是0.5kg,A和B之间的滑动摩擦力为3N.开始时B竖直放置,下端离地面高度h=0.8m,A在B的顶端.现让它们由静止开始自由下落,当木棒与地面相碰后,木棒以竖直向上的速度反向运动.设碰撞时间很短,碰撞无机械能损失,不考虑空气阻力,取当地的重力加速度g=10m/s2.试求:(1)木棒第一次着地时速度的大小;
(2)若在棒第二次着地前,要使A不脱离棒,棒的最小长度是多少?
【答案】分析:分多个阶段进行牛顿第二定律和运动学公式进行计算和判断
解答:解:(1)设B着地前瞬间的速度的大小为v1,释放后A和B相对静止一起做自由落体运动,B着地前瞬间的速度的大小为: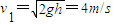
(2)设A.B的质量都为m,B与地面碰撞后,圆环受到重力mg=5N,受到向上的摩擦力f=3N,mg>f所以圆环继续向下做匀加速运动,棒以与着地时相同的速率竖直向上做匀减速运动.根据牛顿第二定律,它们加速度的大小分别为:
aA=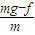 =4m/s2
=4m/s2
aB=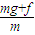 =16m/s2
=16m/s2
当棒到达最高点后,继续以16m/s2的加速度下落,根据竖直上抛和自由落体的对称性,第二次着地时的速度为4m/s,而此时圆环一直加速下落速度肯定大于4m/s,二者不会相对静止,设棒与地面碰撞后向上运动到再次落回地面所需的时间为t: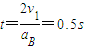
在此时间内圆环的位移: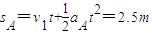
所以在棒第二次着地前,要使圆环不脱离棒,棒的最小长度是2.5m
答:(1)B着地前瞬间的速度大小为4m/s.
(2)在棒第二次着地前,要使A不脱离棒,棒的最小长度是2.5m.
点评:本题的难点是出现了圆环和木棒两个研究对象相对运动,要采取隔离法逐个受力分析运用牛顿第二定律,再选取地面为参照物逐个运用运动学公式
解答:解:(1)设B着地前瞬间的速度的大小为v1,释放后A和B相对静止一起做自由落体运动,B着地前瞬间的速度的大小为:
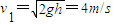
(2)设A.B的质量都为m,B与地面碰撞后,圆环受到重力mg=5N,受到向上的摩擦力f=3N,mg>f所以圆环继续向下做匀加速运动,棒以与着地时相同的速率竖直向上做匀减速运动.根据牛顿第二定律,它们加速度的大小分别为:
aA=
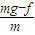 =4m/s2
=4m/s2aB=
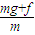 =16m/s2
=16m/s2 当棒到达最高点后,继续以16m/s2的加速度下落,根据竖直上抛和自由落体的对称性,第二次着地时的速度为4m/s,而此时圆环一直加速下落速度肯定大于4m/s,二者不会相对静止,设棒与地面碰撞后向上运动到再次落回地面所需的时间为t:
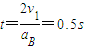
在此时间内圆环的位移:
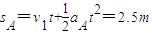
所以在棒第二次着地前,要使圆环不脱离棒,棒的最小长度是2.5m
答:(1)B着地前瞬间的速度大小为4m/s.
(2)在棒第二次着地前,要使A不脱离棒,棒的最小长度是2.5m.
点评:本题的难点是出现了圆环和木棒两个研究对象相对运动,要采取隔离法逐个受力分析运用牛顿第二定律,再选取地面为参照物逐个运用运动学公式

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图所示,一圆环A套在一粗细均匀的圆木棒B上,圆环A的高度相对B的长度可以忽略不计.A和B的质量都是0.5kg,A和B之间的滑动摩擦力为3N.开始时B竖直放置,下端离地面高度h=0.8m,A在B的顶端.现让它们由静止开始自由下落,当木棒与地面相碰后,木棒以竖直向上的速度反向运动.设碰撞时间很短,碰撞无机械能损失,不考虑空气阻力,取当地的重力加速度g=10m/s2.试求:
如图所示,一圆环A套在一粗细均匀的圆木棒B上,圆环A的高度相对B的长度可以忽略不计.A和B的质量都是0.5kg,A和B之间的滑动摩擦力为3N.开始时B竖直放置,下端离地面高度h=0.8m,A在B的顶端.现让它们由静止开始自由下落,当木棒与地面相碰后,木棒以竖直向上的速度反向运动.设碰撞时间很短,碰撞无机械能损失,不考虑空气阻力,取当地的重力加速度g=10m/s2.试求: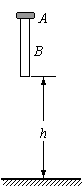
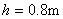 ,A在B的顶端.现让它们由静止开始自由下落,当木棒与地面相碰后,木棒以竖直向上的速度反向运动.设碰撞时间很短,碰撞无机械能损失,不考虑空气阻力,取当地的重力加速度g取l0m/s2.试求:
,A在B的顶端.现让它们由静止开始自由下落,当木棒与地面相碰后,木棒以竖直向上的速度反向运动.设碰撞时间很短,碰撞无机械能损失,不考虑空气阻力,取当地的重力加速度g取l0m/s2.试求: