题目内容
( 18分)如图,在直角坐标系xOy平面内,虚线MN平行于y轴,N 点坐标(-L,0),MN与y轴之间有沿y 轴正方向的匀强电场,在第四象限的某区域有方向垂直于坐标平面的圆形有界匀强磁场(图中未画出)。现有一质量为m、电荷量为e的电子,从虚线MN上的P点,以平行于x 轴正方向的初速度v0射人电场,并从y轴上A点(0,0.5L)射出电场,射出时速度方向与y轴负方向成300角,此后,电子做匀速直线运动,进人磁场并从圆形有界磁场边界上Q点( ,-L )射出,速度沿x轴负方向。不计电子重力。求:
,-L )射出,速度沿x轴负方向。不计电子重力。求:
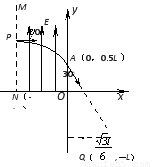
(1)匀强电场的电场强度E的大小?
(2)匀强磁场的磁感应强度B的大小?电子在磁场中运动的时间t是多少?
(3)圆形有界匀强磁场区域的最小面积S是多大?
(1)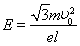 ? (2)
? (2)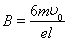 ,
,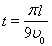 (3)
(3)
【解析】
试题分析:⑴ 设电子在电场中运动的加速度为a,时间为t,离开电场时,沿y轴方向的速度大小为vy,则
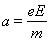 ???????? (1分)
???????? (1分)
vy=at ???????? (1分)
l=v0t? ???????? (1分)
vy=v0cot300 ???????? (1分)
解得 ????????? (2分)
????????? (2分)
(2)设轨迹与x轴的交点为D,OD距离为xD,则
xD=0.5ltan300 ???????? (2分)
xD=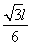 ???????? (1分)
???????? (1分)
所以,DQ平行于y轴,电子在磁场中做匀速圆周运动的轨道的圆心在DQ上,电子运动轨迹如图所示。设电子离开电场时速度为v,在磁场中做匀速圆周运动的轨道半径为r,则
v0=vsin300??????????????????? ? ???????? (1分)
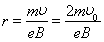 ????????? ?????????? (1分)
????????? ?????????? (1分)
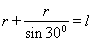 (有
(有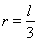 )??????????? (2分)
)??????????? (2分)
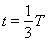 ???????????????????????????? (1分)
???????????????????????????? (1分)
 (或
(或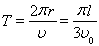 )???????? (1分)
)???????? (1分)
解得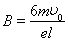 ,
,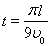 ???????????? (2分)
???????????? (2分)

(3)以切点F、Q为直径的圆形有界匀强磁场区域的半径最小,设为 r1,则
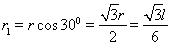 ???????? (2分)
???????? (2分)
 ????????? (1分)
????????? (1分)
考点:本题考查带电粒子在复合场中的运动

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案

 。在所有木块都静止的初始条件下,有一个沿轨道方向水平向右的恒力F持续作用在0号小木块上,使其与后面的木块连接发生碰撞,假如所有碰撞都是完全非弹性的(碰后合为一体共速运动)。求:
。在所有木块都静止的初始条件下,有一个沿轨道方向水平向右的恒力F持续作用在0号小木块上,使其与后面的木块连接发生碰撞,假如所有碰撞都是完全非弹性的(碰后合为一体共速运动)。求:
 米,那么在2号木块被碰撞后的瞬间,系统的总动能为多少?
米,那么在2号木块被碰撞后的瞬间,系统的总动能为多少? 米的前提下,为了保持正在运动的物块系统在每次碰撞之前的瞬间其总动能都为一个恒定的数值,那么我们应该设计第
米的前提下,为了保持正在运动的物块系统在每次碰撞之前的瞬间其总动能都为一个恒定的数值,那么我们应该设计第 号和第n号木块之间距离
号和第n号木块之间距离 为多少米?
为多少米?