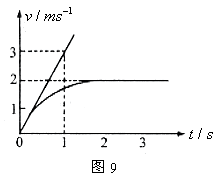题目内容
如图所示,一块质量为M、长为l的匀质板放在很长的水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮并与桌面平行,某人以恒定的速度v向下拉绳,物块最多只能到达板的中点,且此时板的右端距离桌边定滑轮足够远.求:
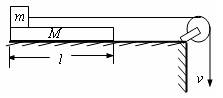
(1)若板与桌面间光滑,物块与板的动摩擦因数及物块刚到达板的中点时板的位移.
(2)若板与桌面间有摩擦,为使物块能到达板右端,板与桌面的动摩擦因数的范围.
.

(1)若板与桌面间光滑,物块与板的动摩擦因数及物块刚到达板的中点时板的位移.
(2)若板与桌面间有摩擦,为使物块能到达板右端,板与桌面的动摩擦因数的范围.
.
(1) (2)μ2≥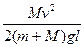
(1)板在摩擦力作用下向右做匀加速运动直至与物块速度相同,此时物块刚到达板的中点,设木板加速度为a1,运动时间为t1,
对木板有μ1mg = Ma、
v = a1t1
∴t1 =
设在此过程中物块前进位移为s1,板前进位移为s2,则
s1 = vt1、
s2 =t1
又因为s1-s2 = ,
由以上几式可得
物块与板间的动摩擦因数μ1= 、
板的位移s2 = .
(2)设板与桌面间的动摩擦因数为μ2,物块在板上滑行的时间为t2,木板的加速度为a2,对板有μ1mg — μ2(m + M) g = Ma2,
且v = a2t2
解得t2 =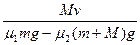
又设物块从板的左端运动到右端的时间为t3,则
vt3 —t3 = l,
t3 =
为了使物块能到达板的右端,必须满足t2 ≥ t3
即 ,
,
则μ2≥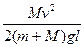
所以为了使物块能到达板的右端,板与桌面间的摩擦因数μ2≥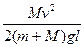
对木板有μ1mg = Ma、
v = a1t1
∴t1 =
设在此过程中物块前进位移为s1,板前进位移为s2,则
s1 = vt1、
s2 =t1
又因为s1-s2 = ,
由以上几式可得
物块与板间的动摩擦因数μ1= 、
板的位移s2 = .
(2)设板与桌面间的动摩擦因数为μ2,物块在板上滑行的时间为t2,木板的加速度为a2,对板有μ1mg — μ2(m + M) g = Ma2,
且v = a2t2
解得t2 =
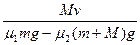
又设物块从板的左端运动到右端的时间为t3,则
vt3 —t3 = l,
t3 =
为了使物块能到达板的右端,必须满足t2 ≥ t3
即
 ,
,则μ2≥
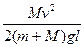
所以为了使物块能到达板的右端,板与桌面间的摩擦因数μ2≥

练习册系列答案
相关题目

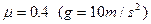


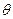 的长斜面上有一带风帆的滑块,从静止开始沿斜面下滑,滑块质量为m,它与斜面间的动摩擦因数为
的长斜面上有一带风帆的滑块,从静止开始沿斜面下滑,滑块质量为m,它与斜面间的动摩擦因数为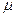 ,帆受到的空气阻力与滑块下滑速度的大小成正比,即
,帆受到的空气阻力与滑块下滑速度的大小成正比,即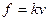 。
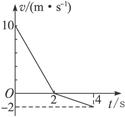
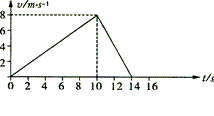
。 ,从静止下滑的速度图象如图所示的曲线,图中直线是t=0时的速度图线的切线,由此求出
,从静止下滑的速度图象如图所示的曲线,图中直线是t=0时的速度图线的切线,由此求出