题目内容
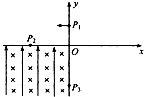 (2007?徐州模拟)如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向.在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场.一质量为m、电荷量为q的带电质点,从y轴上y=h处的P1点以一定的水平初速度沿x轴负方向进入第二象限.然后经过x轴上x=-2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动.之后经过y轴上y=-2h处的P3点进入第四象限.已知重力加速度为g.求:
(2007?徐州模拟)如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向.在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场.一质量为m、电荷量为q的带电质点,从y轴上y=h处的P1点以一定的水平初速度沿x轴负方向进入第二象限.然后经过x轴上x=-2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动.之后经过y轴上y=-2h处的P3点进入第四象限.已知重力加速度为g.求:(1)质点到达P2点时速度的大小和方向;
(2)第三象限空间中电场强度和磁感应强度的大小;
(3)若在第四象限加一匀强电场,使质点做直线运动,求此电场强度的最小值.
分析:带电粒子先做平抛运动,将运动分解成水平方向匀速直线运动与竖直方向自由落体运动,从而求出抛出速度的大小与方向.当带电粒子进入电场、磁场与重力场中时,重力与电场力相平衡,洛伦兹力提供向心力使其做匀速圆周运动,由平衡可得出电场强度大小,再几何关系可求出磁感应强度大小.最后粒子进入电场与重力场中时,做直线运动.要使电场力最小,且电场力和重力的合力与速度在一条直线上,所以电场强度方向与速度方向相垂直.
解答: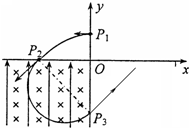 解:(1)质点从P1到P2,由平抛运动规律
解:(1)质点从P1到P2,由平抛运动规律
h=
gt2
v0=
vy=gt
求出 v=
=2
方向与x轴负方向成45°角
(2)质点从P2到P3,重力与电场力平衡,洛仑兹力提供向心力
Eq=mg
Bqv=m
由几何关系得:(2R)2=(2h)2+(2h)2
解之得E=
B=
(3)质点进入第四象限做直线运动,当电场强度的方向与运动方向垂直时电场强度最小,
由qE'=mg?cos45°
得:E′=
 解:(1)质点从P1到P2,由平抛运动规律
解:(1)质点从P1到P2,由平抛运动规律h=
| 1 |
| 2 |
v0=
| 2h |
| t |
求出 v=
| v02+vy2 |
| gh |
方向与x轴负方向成45°角
(2)质点从P2到P3,重力与电场力平衡,洛仑兹力提供向心力
Eq=mg
Bqv=m
| v2 |
| R |
由几何关系得:(2R)2=(2h)2+(2h)2
解之得E=
| mg |
| q |
B=
| m |
| q |
|
(3)质点进入第四象限做直线运动,当电场强度的方向与运动方向垂直时电场强度最小,
由qE'=mg?cos45°
得:E′=
| ||
| 2q |
点评:本题考查带电粒子在场中两运动模型:匀速圆周运动与平抛运动,及相关的综合分析能力,以及空间想像的能力,应用数学知识解决物理问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2007?徐州模拟)如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,关于这列波有以下说法,其中正确的是( )
(2007?徐州模拟)如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,关于这列波有以下说法,其中正确的是( )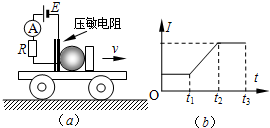 (2007?徐州模拟)压敏电阻的阻值随所受压力的增大而减小,有位同学利用压电陶瓷设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压电陶瓷和一块挡板固定在绝缘小车上,中间放置一个绝缘重球,它的直径略小于陶瓷和挡板间的距离.小车向右做直线运动过程中,电压流表示数如图(b)所示,下列判断正确的是( )
(2007?徐州模拟)压敏电阻的阻值随所受压力的增大而减小,有位同学利用压电陶瓷设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压电陶瓷和一块挡板固定在绝缘小车上,中间放置一个绝缘重球,它的直径略小于陶瓷和挡板间的距离.小车向右做直线运动过程中,电压流表示数如图(b)所示,下列判断正确的是( ) (2007?徐州模拟)如图所示,A、B是一条电场线上的两点,若在A点释放一初速为零的电子,电子仅受电场力作用,沿电场线从A运动到B.则( )
(2007?徐州模拟)如图所示,A、B是一条电场线上的两点,若在A点释放一初速为零的电子,电子仅受电场力作用,沿电场线从A运动到B.则( )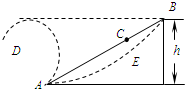 (2007?徐州模拟)如图所示,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )
(2007?徐州模拟)如图所示,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )