Question

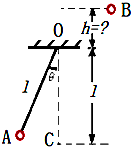如图所示，将质量为m的小球A做成单摆，让小球A从静止释放的同时，高出悬点O的另一小球B做自由落体运动，结果它们同时到达跟单摆的平衡位置C等高处．已知摆长为l，偏角θ＜5°．求：
（1）小球B的初位置与单摆悬点之间的高度差h；
（2）小球A到达最低点C时的速度VC；
（3）小球A到达最低点C时，摆线所受的拉力F的大小．

Answer 1

分析：1、小球A做单摆运动，根据单摆周期公式求出小球A从A→C的时间，
小球B做自由落体运动，根据自由落体运动的规律列出等式求解．
2、根据小球A到达最低点C过程中机械能守恒列出等式求解．
3、小球A在最低点C处，根据牛顿第二定律求解．

解答：解：（1）从小球释放到同时到达跟单摆的平衡位置C等高处，
A、B经历的时间：t_A=t_B　　　　　　　
小球A做单摆运动，t_A=（2n-1）

TA

4

  其中n=1、2、3、…
根据单摆周期公式得T_A=2π

l g

小球B做自由落体运动，
h+l=

1

2

g

t

2 B

联立求解：h=

π2(2n-1)2l

8

-l，其中n=1、2、3、…
（2）根据小球A到达最低点C过程中机械能守恒列出等式：
mgl（1-cosθ）=

1

2

m

v

2 C

v_C=

2gl(1-cosθ)

（3）小球A在最低点C处，根据牛顿第二定律得：
F-mg=m

V 2 C

l

，
解得：F=（3-2cosθ）mg 
答：（1）小球B的初位置与单摆悬点之间的高度差h=

π2(2n-1)2l

8

-l，其中n=1、2、3、…；
（2）小球A到达最低点C时的速度大小是

2gl(1-cosθ)

；
（3）小球A到达最低点C时，摆线所受的拉力F的大小是（3-2cosθ）mg．

点评：该题考查了单摆周期公式，机械能守恒，牛顿第二定律的应用，由于单摆具有周期性，所以解这类题时要注意由于振动的周期性而引起的多解．