题目内容
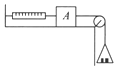
【题目】如图甲,PNQ为竖直放置的半径为0.1 m的半圆形轨道,在轨道的最低点P和最高点Q各安装了一个压力传感器,可测定小球在轨道内侧通过这两点时对轨道的压力FP和FQ.轨道的下端与一光滑水平轨道相切,水平轨道上有一质量为0.06 kg的小球A,以不同的初速度v0与静止在轨道最低点P处稍右侧的另一质量为0.04 kg的小球B发生碰撞,碰后形成一整体(记为小球C)以共同速度v冲入PNQ轨道.(A、B、C三小球均可视为质点,g取10 m/s2)
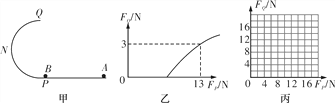
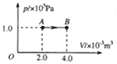
(1)若FP和FQ的关系图线如图乙所示,求:当FP=13 N时所对应的入射小球A的初速度v0为多大?
(2)当FP=13 N时,AB所组成的系统从A球开始向左运动到整体达到轨道最高点Q全过程中所损失的总机械能为多少?
(3)若轨道PNQ光滑,小球C均能通过Q点.试推导FP随FQ变化的关系式,并在图丙中画出其图线.
【答案】(1)![]() (2)0.6 J (3) FQ=FP-6(N)
(2)0.6 J (3) FQ=FP-6(N) 
【解析】试题分析:小球经过P、Q两点时,由重力和轨道对小球的支持力的合力提供向心力,AB相碰,满足动量守恒,根据牛顿第二定律及动量守恒定律列式即可求出速度;先求出AB相碰所损失的机械能,根据动能定理求出从球C从P运动至Q的过程中摩擦力做功,进而求出小球损失的机械能;轨道光滑,小球C由P至Q的过程中机械能守恒,可列出小球经过AC两点的速度关系,再由牛顿第二定律得到FP随FQ变化的关系式,画出图线。
(1)设A球的质量为M,B球的质量为m,由牛顿第三定律可知,小球在P、Q两点所受轨道的弹力大小为:NP=FP,NQ=FQ
在P点根据牛顿第二定律可得: ![]()
带入数据解得: ![]()
A、B相碰过程中满足动量守恒:Mv0=(M+m)vP
带入数据解得: ![]()
(2) A、B相碰所损失的机械能: ![]()
带入数据解得: ![]()
球C在Q点由牛顿第二定律得: ![]()
球C从P运动至Q的过程,根据动能定理得: ![]()
联立并代入数据解得:Wf=-0.2 J
故球C上升过程中所损失的机械能ΔE2=0.2 J
故整个系统在全过程中所损失的机械能ΔE=ΔE1+ΔE2=0.6 J
(3)因轨道光滑,小球C由P至Q的过程中根据动能定理得:
![]()
联立解得:NP-NQ=6(M+m)g
即FQ=FP-6(N)
图线如图所示