题目内容
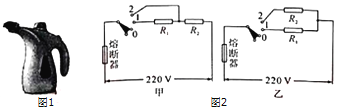
【题目】如图甲所示,质量M=1kg的薄木板静止在水平面上,质量m=1kg的铁块静止在木板的右端,可视为质点。设最大静摩擦力等于滑动摩擦力,取g=10m/s2。现给铁块施加一个水平向左的力F。
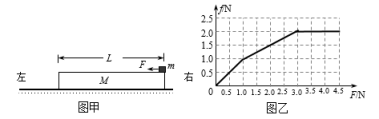
(1)若力F从零开始逐渐增加,且铁块始终在木板上没有掉下来,铁块受到的摩擦力f随力F大小变化的图象如图乙所示,求木板与水平面间的动摩擦因数μ1和铁块与木板之间的动摩擦因数μ2
(2)在第(1)问的基础上,若力F为恒力4N,作用1s后撤去F,最终发现铁块恰好能运动到木板的左端,求木板的长度L
【答案】(1)μ1=0.05;μ2=0.2(2)![]() m
m
【解析】
试题分析:(1)从图乙中可以看出,当F从3N逐渐增加到4.5N时,f不变,则此时的f是滑动摩擦力,即f=μ2mg
解得 μ2=0.2
由图乙可知,当力F从1N逐渐增加到3N时,铁块和木板相对静止,并且一起加速运动,当F=2N时铁块所受摩擦力为fm=1.5N,因此可求出铁块的加速度为
![]() (am=0.5m/s2)
(am=0.5m/s2)
木板的加速度此时也为aM=am
对整体运用由牛顿第二定律 F-μ1(mg+Mg)=(M+m)aM
解得 μ1=0.05
(2)(13分)当F=4N时,铁块的加速度为
由牛顿第二定律 F-f1=mam1 (am1=2m/s2)
木板的加速度为aM1 则 f1-μ1(mg+Mg)=MaM1 (aM1=1m/s2)
因此在t=1s内
Sm=![]() am1t2 ,Sm =1m
am1t2 ,Sm =1m
SM=![]() aM1t2,SM =0.5m
aM1t2,SM =0.5m
在t=1s时
vm=am1t=2m/s
vM=aM1t=1m/s
在此后,铁块减速,其加速度为am2 则μ2mg=mam2 得am2=2m/s2
木板加速,其加速度为aM2 则
μ2mg-μ1(mg+Mg)=MaM2 得aM2=1m/s2
当两者达到共同速度时v=vm-am2t′=vM+aM2t′ 得t′=![]() s,v=
s,v=![]() m/s
m/s
从撤去力F到两者达到共同速度的过程中,铁块的位移
Sm1=![]() 得Sm1=
得Sm1=![]() m
m
木板的位移 SM2=![]() 得SM2=
得SM2=![]() m
m
则木板长度为 L=(Sm- SM)+(Sm1- SM2)
解得 L=![]() m
m

 孟建平名校考卷系列答案
孟建平名校考卷系列答案