题目内容
17. 如图,质量分别为mA、mB的A、B两小球带有同种电荷,电荷量分别为qA、qB,用绝缘细线悬挂在水平天花板上.平衡时,两小球恰处于同一水平位置,细线与竖直方向间夹角分别为α与β(α>β).现突然让两小球失去各自所带电荷,接着开始摆动,摆动过程中最大速度分别为vA、vB,最大动能分别为EkA、EkB.则( )
如图,质量分别为mA、mB的A、B两小球带有同种电荷,电荷量分别为qA、qB,用绝缘细线悬挂在水平天花板上.平衡时,两小球恰处于同一水平位置,细线与竖直方向间夹角分别为α与β(α>β).现突然让两小球失去各自所带电荷,接着开始摆动,摆动过程中最大速度分别为vA、vB,最大动能分别为EkA、EkB.则( )| A. | mA一定小于mB | B. | qA一定大于qB | C. | vA一定大于vB | D. | EkA一定小于EkB |
分析 设两个球间的静电力为F,分别对两个球受力分析,求解重力表达式后比较质量大小;根据机械能守恒定律列式求解后比较最低点速度大小,再进一步比较动能大小.
解答  解:A、对小球A受力分析,受重力、静电力、拉力,如图
解:A、对小球A受力分析,受重力、静电力、拉力,如图
根据平衡条件,有:${m}_{A}g=\frac{F}{tan{θ}_{1}}$
故:${m}_{A}=\frac{F}{g•tan{θ}_{1}}$
同理,有:${m}_{B}=\frac{F}{g•tan{θ}_{2}}$
由于θ1>θ2,故mA<mB,故A正确;
B、两球间的库仑力是作用力与反作用力,一定相等,与两个球是否带电量相等无关,故B错误;
C、小球摆动过程机械能守恒,有${m}_{A}g△h=\frac{1}{2}m{v}_{A}^{2}$,解得${v}_{A}=\sqrt{2g•△h}$,由于A球摆到最低点过程,下降的高度△h较大,故A球的速度较大,故C正确;
D、小球摆动过程机械能守恒,有mg△h=EK,故
Ek=mg△h=mgL(1-cosθ)=$\frac{F}{tanθ}$L(1-cosθ)
其中L、cosθ相同,根据数学中的半角公式,得到:
Ek=$\frac{F}{tanθ}$L(1-cosθ)=$FLcosθ\frac{1-cosθ}{sinθ}=FLcosθ•tan\frac{θ}{2}$
其中Lcosθ=h,相同,故θ越大,$tan\frac{θ}{2}$越大,动能越大,故EkA一定大于EkB,故D错误;
故选:AC.
点评 本题关键分别对两个小球受力分析,然后根据平衡条件列方程;再结合机械能守恒定律列方程分析求解.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7. 人造地球卫星绕地球的运动可看成匀速圆周运动,它们做匀速圆周运动的线速度会随着轨道半径的变化而变化,现测得不同人造地球卫星的线速度V与轨道半径r的关系如图所示,已知引力常量为G,则可求得地球质量为( )
人造地球卫星绕地球的运动可看成匀速圆周运动,它们做匀速圆周运动的线速度会随着轨道半径的变化而变化,现测得不同人造地球卫星的线速度V与轨道半径r的关系如图所示,已知引力常量为G,则可求得地球质量为( )
 人造地球卫星绕地球的运动可看成匀速圆周运动,它们做匀速圆周运动的线速度会随着轨道半径的变化而变化,现测得不同人造地球卫星的线速度V与轨道半径r的关系如图所示,已知引力常量为G,则可求得地球质量为( )
人造地球卫星绕地球的运动可看成匀速圆周运动,它们做匀速圆周运动的线速度会随着轨道半径的变化而变化,现测得不同人造地球卫星的线速度V与轨道半径r的关系如图所示,已知引力常量为G,则可求得地球质量为( )| A. | $\frac{Ga}{b}$ | B. | $\frac{Gb}{a}$ | C. | $\frac{a}{Gb}$ | D. | $\frac{b}{Ga}$ |
8. 如图所示,一轻质弹簧一端固定,另一端与物体A相连接并使A在光滑水平面上做简谐运动,当A到达最大位移处时,把物块B由静止放置在A上面,此后A、B保持相对静止,共同做简谐运动,下列说法正确的是( )
如图所示,一轻质弹簧一端固定,另一端与物体A相连接并使A在光滑水平面上做简谐运动,当A到达最大位移处时,把物块B由静止放置在A上面,此后A、B保持相对静止,共同做简谐运动,下列说法正确的是( )
 如图所示,一轻质弹簧一端固定,另一端与物体A相连接并使A在光滑水平面上做简谐运动,当A到达最大位移处时,把物块B由静止放置在A上面,此后A、B保持相对静止,共同做简谐运动,下列说法正确的是( )
如图所示,一轻质弹簧一端固定,另一端与物体A相连接并使A在光滑水平面上做简谐运动,当A到达最大位移处时,把物块B由静止放置在A上面,此后A、B保持相对静止,共同做简谐运动,下列说法正确的是( )| A. | 振幅将比原来小 | |
| B. | 经过平衡位置的速度大小和原来相等 | |
| C. | 振子由最大位移处回到平衡位置所用时间和原来相同 | |
| D. | A对B的静摩擦力大小与弹簧形变量成正比 |
12.做曲线运动的物体,可能保持不变的物理量是( )
| A. | 速度 | B. | 合外力 | C. | 动能 | D. | 机械能 |
9. 一定质量的理想气体经历三个变化过程,其压强P与温度T的关系图象如图所示,已知bc平行于纵轴,ca平行于横轴.下列判断正确的是( )
一定质量的理想气体经历三个变化过程,其压强P与温度T的关系图象如图所示,已知bc平行于纵轴,ca平行于横轴.下列判断正确的是( )
 一定质量的理想气体经历三个变化过程,其压强P与温度T的关系图象如图所示,已知bc平行于纵轴,ca平行于横轴.下列判断正确的是( )
一定质量的理想气体经历三个变化过程,其压强P与温度T的关系图象如图所示,已知bc平行于纵轴,ca平行于横轴.下列判断正确的是( )| A. | a→b过程外界对气体做功 | |
| B. | b→c过程气体从外界吸收热量 | |
| C. | c→a过程外界对气体所做的功小于气体放出的热量 | |
| D. | b和c两个状态中,单位面积单位时间气体分子撞击容器壁的次数不同 |
6. 如图所示,闭合开关S后当滑动变阻器的滑片从左向右滑动时,整个电路中的电流I,R1两端的电压U1,R2两端的电压U2的变化情况是( )
如图所示,闭合开关S后当滑动变阻器的滑片从左向右滑动时,整个电路中的电流I,R1两端的电压U1,R2两端的电压U2的变化情况是( )
 如图所示,闭合开关S后当滑动变阻器的滑片从左向右滑动时,整个电路中的电流I,R1两端的电压U1,R2两端的电压U2的变化情况是( )
如图所示,闭合开关S后当滑动变阻器的滑片从左向右滑动时,整个电路中的电流I,R1两端的电压U1,R2两端的电压U2的变化情况是( )| A. | I变大,U1变大,U2变小 | B. | I变小,U1变大,U2变大 | ||
| C. | I变小,U1变大,U2变小 | D. | I变小,U1变小,U2变小 |
7.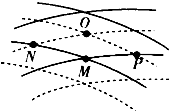 如图所示,实线与虚线分别表示振幅、频率均相同的两列波的波峰和波谷.此刻,M是波峰与波峰的相遇点,下列说法中正确的是( )
如图所示,实线与虚线分别表示振幅、频率均相同的两列波的波峰和波谷.此刻,M是波峰与波峰的相遇点,下列说法中正确的是( )
 如图所示,实线与虚线分别表示振幅、频率均相同的两列波的波峰和波谷.此刻,M是波峰与波峰的相遇点,下列说法中正确的是( )
如图所示,实线与虚线分别表示振幅、频率均相同的两列波的波峰和波谷.此刻,M是波峰与波峰的相遇点,下列说法中正确的是( )| A. | 该时刻位于O处的质点正处于平衡位置 | |
| B. | P、N两处的质点始终处在平衡位置 | |
| C. | 随着时间的推移,M处的质点将向O处移动 | |
| D. | 从该时刻起,经过四分之一周期,M处的质点到达平衡位置,此时位移为零 |
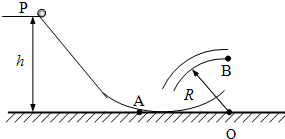 如图所示,轨道由斜直轨道、凹形圆弧轨道和半径R=2.0m的圆弧管道(内径不计)组成,三部分轨道均光滑处于同一竖直平面内,且依次平滑连接,A 点为凹形圆弧轨道的最低点,B点为圆弧管道的最高点,圆弧管道的圆心O点与A点处在同一水平面上.一质量m=0.10kg、可视为质点的小球从斜直轨道上的P点无初速滑下,经过A点向B点运动,P点距A点所在水平面的高度h=2.5m,不计一切阻力,g=9.8m/s2.
如图所示,轨道由斜直轨道、凹形圆弧轨道和半径R=2.0m的圆弧管道(内径不计)组成,三部分轨道均光滑处于同一竖直平面内,且依次平滑连接,A 点为凹形圆弧轨道的最低点,B点为圆弧管道的最高点,圆弧管道的圆心O点与A点处在同一水平面上.一质量m=0.10kg、可视为质点的小球从斜直轨道上的P点无初速滑下,经过A点向B点运动,P点距A点所在水平面的高度h=2.5m,不计一切阻力,g=9.8m/s2.