��Ŀ����
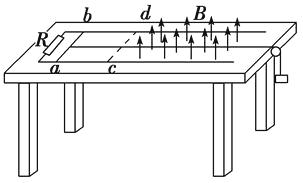
����Ŀ����ͼ��ʾ�����ΪL�������㹻���Ĺ⻬ƽ�н�������MN��PQ��ˮƽ��нǦ�=30�㣬�¶�N��Q������һ��ֵΪR�ĵ��裮��������һ������������abcd��cd���´��ڴŸ�Ӧǿ�ȴ�СΪB������ֱ����ƽ�����µ���ǿ�ų�������ΪL������Ϊr�Ľ������뵼��Ӵ������Ҵ�ֱ������ã�����������abλ���ɾ�ֹ�ͷŵ�ͬʱ���Խ�����ʩ��һ��ƽ�е������µĺ���F��F�Ĵ�С�ǽ����������� ![]() ��������ͨ��cdʱǡ���������˶�������ʱͻȻֻ����F�ķ�������F�Ĵ�С���䣬����һ��ʱ����������ֹ����֪�������ٶ�Ϊg�����ƽ�������ĵ��裬��
��������ͨ��cdʱǡ���������˶�������ʱͻȻֻ����F�ķ�������F�Ĵ�С���䣬����һ��ʱ����������ֹ����֪�������ٶ�Ϊg�����ƽ�������ĵ��裬��
��1����������������
��2�����������е���R�ϲ����Ľ����ȣ�
��3��������ͨ��cd�������˶��������룮
���𰸡�
��1��
�⣺�ڴų����˶����̣� ![]() ��
�� ![]()
�ս���ų�ʱ�� ![]() ��
��
![]()
�������Եõ��� ![]()
��2��
�⣺�ӽ���������ų������վ�ֹ�����У�
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()
�������Եõ��� ![]()
��3��
�⣺���������������ܺ������ڰ��������� ![]()
ȡ����ʱ���t�ڣ���x=v��t�� ![]()
���벢����õ��� ![]()
��������뿪cd�������˶���������Ϊx�������ۻ�������֪���� ![]()
�������Եõ���x=2L
����������1����ţ�ٵڶ����ɺ��˶�ѧ��ʽ����������ս���ų�ʱ���ٶȣ��ս���ų���ƽ������������������2����������ϵ�������������е���R�ϲ����Ľ����ȣ���3����F������������ܵĺ������ڰ�����������ţ�ٵڶ�������ʽ�����ۻ�����������˶��������룻
�����㾫����������Ҫ�����˶��ܶ������ۺ�Ӧ�úͽ������ɵ����֪ʶ�㣬��Ҫ����Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ���������:Q=I2Rt��ʽ��Q��ʾ����ͨ�������������������λ��J.�������������ǶԴ������·���ǶԷǴ������·�������õIJ�����ȷ�����⣮