��Ŀ����
3�� ��ͼ��ʾ������ΪL�Ĵֲ�ƽ�н�������PQ��P��Q����б���ã�����QQ��֮������һ����ֵΪR�ĵ���Ϳ���S����PP�䴦��һС��ˮƽ����ù⻬Բ����������֪��PP�������ĸ߶�Ϊh����б���촦�ڴ�ֱ�ڵ���ƽ�����ǿ�ų���ͼ��δ�������У����Ͽ�����S����һ������Ϊm������Ϊr����ΪL�Ľ�������AA�䴦��ֹ��ʼ���£���������ص���PP���ˮƽ����Ϊx1�����պϿ���S�����������Դ�AA�䴦��ֹ��ʼ���£����������ص���PP���ˮƽ����Ϊx2�����Ƶ�����裬���Խ���������PP�䴦��������ʧ���������ٶ�Ϊg����
��ͼ��ʾ������ΪL�Ĵֲ�ƽ�н�������PQ��P��Q����б���ã�����QQ��֮������һ����ֵΪR�ĵ���Ϳ���S����PP�䴦��һС��ˮƽ����ù⻬Բ����������֪��PP�������ĸ߶�Ϊh����б���촦�ڴ�ֱ�ڵ���ƽ�����ǿ�ų���ͼ��δ�������У����Ͽ�����S����һ������Ϊm������Ϊr����ΪL�Ľ�������AA�䴦��ֹ��ʼ���£���������ص���PP���ˮƽ����Ϊx1�����պϿ���S�����������Դ�AA�䴦��ֹ��ʼ���£����������ص���PP���ˮƽ����Ϊx2�����Ƶ�����裬���Խ���������PP�䴦��������ʧ���������ٶ�Ϊg������1�����ضϿ�ʱ���������뿪��PP����ٶȴ�С��
��2���Ƚ�ǰ�����ν������뵼��Ħ��������������С��
��3�����رպ�ʱ�����������»������в����Ľ����ȣ�
���� ��1���������뿪��PP�����ƽ���˶�����֪ˮƽ����߶ȣ�����ƽ���˶���֪ʶ���������������PP����ٶȴ�С��
��2���������뵼��Ħ���������������ڿ˷�Ħ�����������ɹ��ܹ�ϵ���
��3�����رպϺ������»�ʱ����Ҫ�˷��������������������ȣ����������غ㶨����⣮
��� �⣺��1�����ضϿ�ʱ���������뿪��PP����ٶȴ�СΪv1���ڿ����˶���ʱ��Ϊt����
x1=v1t
h=$\frac{1}{2}$gt2��
�ɵã�v1=x1$\sqrt{\frac{g}{2h}}$
��2���������뵼��Ħ���������������ڿ˷�Ħ����������ǰ�����ν��������ܵĻ���Ħ�������䣬ͨ����λ�Ʋ��䣬�˷�Ħ����������ȣ�����ǰ�����ν������뵼��Ħ��������������ȣ�
��3�����ضϿ�ʱ���ڽ���������б�����»��Ĺ����У���������ΪWG��Ħ��������ΪWf��
���ݶ��ܶ�����WG+WF=$\frac{1}{2}m{v}_{1}^{2}$
���رպ�ʱ���������뿪��PP����ٶȣ�v2=x2$\sqrt{\frac{g}{2h}}$
�ڽ���������б�����»��Ĺ����У�����������Ħ���������뿪�ضϿ�ʱ��ͬ������������ΪW����ϵͳ�����Ľ�����ΪQ��
�ɶ��ܶ����ɵã�WG+Wf+W��=$\frac{1}{2}m{v}_{2}^{2}$
����ΪQ=|W��|
�����������Ľ����� Qr=$\frac{r}{R+r}$Q
�����������̿ɵã�Qr=$\frac{r}{R+r}$•$\frac{mg}{4h}$��${x}_{1}^{2}-{x}_{2}^{2}$ ����
�𣺣�1�����ضϿ�ʱ���������뿪��PP����ٶȴ�С��x1$\sqrt{\frac{g}{2h}}$��
��2��ǰ�����ν������뵼��Ħ��������������С��ȣ�
��3�����رպ�ʱ�����������»������в����Ľ�������$\frac{r}{R+r}$•$\frac{mg}{4h}$��${x}_{1}^{2}-{x}_{2}^{2}$ ����
���� ��������Ҫ����ƽ���˶����о���������������������غ㶨��������������dz��õ�˼·��ƽʱҪ���ǿ�ⷽ�����ϰ���������գ�

 ���ݼ���ϵ�д�
���ݼ���ϵ�д� 2012��7��11�����磬�й��վ���һ���б��ݶӡ��վ���ɡ�˶�������������������˾��ʷ��к���ɡ���ݣ��ڱ����У���һ���б��ݶӵ�6�ܱ��ݻ����ֶ��Σ�ֱ�̲�������18�����Ѷȶ�������ͼ1��ʾ�����й��ڷɻ��˶������˵������ȷ���ǣ�������
2012��7��11�����磬�й��վ���һ���б��ݶӡ��վ���ɡ�˶�������������������˾��ʷ��к���ɡ���ݣ��ڱ����У���һ���б��ݶӵ�6�ܱ��ݻ����ֶ��Σ�ֱ�̲�������18�����Ѷȶ�������ͼ1��ʾ�����й��ڷɻ��˶������˵������ȷ���ǣ�������| A�� | �����ϵ��˿����ɻ��ɹ������Ե���Ϊ�ο�ϵ | |
| B�� | ����Ա��������̨����ӹ������Էɻ�Ϊ�ο�ϵ | |
| C�� | �Ա����ijһ�ɻ�Ϊ�ο�ϵ�������ɻ����˶��� | |
| D�� | �Ա����ijһ�ɻ�Ϊ�ο�ϵ�������ɻ��Ǿ�ֹ�� |
| A�� | ��O��A��B������B�������� | |
| B�� | ����������Ӵ�B���˶���A�㣬�糡�������� | |
| C�� | BO��ĵ��Ʋ��OA��ĵ��Ʋ��$\frac{m{{v}_{0}}^{2}}{q}$ | |
| D�� | BO��ĵ��Ʋ��OA��ĵ��Ʋ��$\frac{2m{{v}_{0}}^{2}}{q}$ |
 ��ͼ��ʾ��A��B��C������ͬ��λ�����ҷֱ���vA��vB��vC��ˮƽ���ٶ��׳�����С��A��B��C������A��B��ͬһ��ֱ���ϣ�B��C��ͬһˮƽ���ϣ�����С���ͬʱ���ڵ����ϵ�D�㣬���ƿ�������������루������
��ͼ��ʾ��A��B��C������ͬ��λ�����ҷֱ���vA��vB��vC��ˮƽ���ٶ��׳�����С��A��B��C������A��B��ͬһ��ֱ���ϣ�B��C��ͬһˮƽ���ϣ�����С���ͬʱ���ڵ����ϵ�D�㣬���ƿ�������������루������| A�� | ��ͬʱ�׳�A��B�������׳�C�� | B�� | ��ͬʱ�׳�B��C�������׳�A�� | ||
| C�� | ��������vA��vB��vC | D�� | ��������vA��vB��vC |
 һ�����������ֻ�ڵ糡����������x�������˶����������E��λ��x�仯�Ĺ�ϵ��ͼ��ʾ������0-x2���ǶԳƵ����ߣ�Ϊx2-x3����ֱ�ߣ�������˵����ȷ���ǣ�������
һ�����������ֻ�ڵ糡����������x�������˶����������E��λ��x�仯�Ĺ�ϵ��ͼ��ʾ������0-x2���ǶԳƵ����ߣ�Ϊx2-x3����ֱ�ߣ�������˵����ȷ���ǣ�������| A�� | ��xl��x3�������ӵļ��ٶ�һֱ���� | |
| B�� | ��x1��x3�������ӵ��ٶ�һֱ��С | |
| C�� | ������0-x2�����ȱ����˶���x2-x3��������ֱ���˶� | |
| D�� | x1��x2��x3�����Ʀ�1����2����3�Ĺ�ϵΪ��1����2����3 |
| A�� | $\frac{{I}_{1}}{{U}_{1}}$ | B�� | $\frac{{U}_{1}}{{I}_{1}}$ | C�� | $\frac{{U}_{1}}{{I}_{2}}$ | D�� | $\frac{{U}_{1}}{{I}_{1}-{I}_{2}}$ |
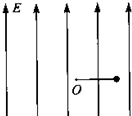 ��ͼ��ʾ���ռ������ǿ��E=$\frac{3mg}{q}$������ֱ���ϵ���ǿ�糡���ڵ糡��һ��Ϊl�ľ�Եϸ�ߣ�һ�˹̶���O�㣬һ��˩������m�������q��С���ֽ�ϸ����ֱ��ˮƽλ�ã�ʹС���ɾ�ֹ�ͷţ���С���˶���ߵ�ʱϸ���ܵ�������ǡ�ôﵽ���ܳ��ܵ����ֵ�����ѣ���
��ͼ��ʾ���ռ������ǿ��E=$\frac{3mg}{q}$������ֱ���ϵ���ǿ�糡���ڵ糡��һ��Ϊl�ľ�Եϸ�ߣ�һ�˹̶���O�㣬һ��˩������m�������q��С���ֽ�ϸ����ֱ��ˮƽλ�ã�ʹС���ɾ�ֹ�ͷţ���С���˶���ߵ�ʱϸ���ܵ�������ǡ�ôﵽ���ܳ��ܵ����ֵ�����ѣ���