题目内容
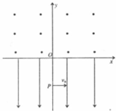 如图所示,在y<0的空间中,存在沿y轴负方向的匀强电场,电场强度E=10N/c;在y>0的空间中,存在垂直xOy平面方向向外的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷g/m=50C/kg),在y=-0.1m处的P点以v0=10m/s的初速度沿x轴正方向开始运动,不计带电粒子的重力,求:
如图所示,在y<0的空间中,存在沿y轴负方向的匀强电场,电场强度E=10N/c;在y>0的空间中,存在垂直xOy平面方向向外的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷g/m=50C/kg),在y=-0.1m处的P点以v0=10m/s的初速度沿x轴正方向开始运动,不计带电粒子的重力,求:(1)带电粒子开始运动后,第一次通过x轴时距O点的距离;
(2)带电粒子进入磁场后,经多长时间返回电场;
(3)带电粒子开始运动后,第二次通过x轴时距O点的距离是多少?如果想使粒子返回到P点,在其它物理量不变的情况下,磁感应强度B应为多少?
分析:(1)粒子从P点抛出后在电场中做类平抛运动,根据平抛运动的基本公式即可求解;
(2)粒子进入磁场后做匀速圆周运动,找出圆心,画出轨迹,求出圆心角,根据圆心角与周期的关系即可求得运动时间;
(3)根据几何关系可求出粒子在磁场中运动回到x轴时运动圆弧对应的弦长,减去第一次通过x轴时距O点的距离既是第二次通过x轴时距O点的距离;
(2)粒子进入磁场后做匀速圆周运动,找出圆心,画出轨迹,求出圆心角,根据圆心角与周期的关系即可求得运动时间;
(3)根据几何关系可求出粒子在磁场中运动回到x轴时运动圆弧对应的弦长,减去第一次通过x轴时距O点的距离既是第二次通过x轴时距O点的距离;
解答:解:(1)粒子在第一象限做类平抛运动,加速度a=
=500m/s2 ①
沿电场方向做匀加速直线运动,由y=
at2得:
运动时间t1=
=
s=
s
沿x轴方向的位移x=v0t1=0.2m
(2)粒子通过y轴进入磁场时在y方向上的速度vy=at1=10 m/s
因此,tanθ=
=
=1,θ=45°
粒子在第二象限以O′为圆心做匀速圆周运动,圆弧所对的圆心角为α=270°,
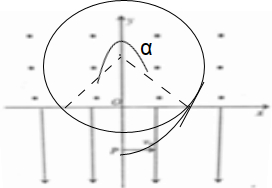
运动时间t2=
T=
②
T=
=
×
S=
S ③
②③联立得:t2=
s
(3)类平抛运动的水平位移:x1=v0t1=10×
m=0.2m
匀速圆周运动洛伦兹力提供向心力,即qvB=m
④
v=
v0=10
m/s ⑤
④⑤联立得:r=
m
由几何关系得匀速圆周运动的弦长:L=2rsin45°=
×
×2=0.8m
第二次通过x轴时距O点的距离是x2=L-x1=8-2m=6m
要让粒子再次回到P点,弦长L应为2x1
则粒子作圆周运动的半径R′=
=
m=0.2
m
由qvB=m
得:B′=
=1T
答;(1)带电粒子开始运动后,第一次通过x轴时距O点的距为0.2m;
(2)带电粒子进入磁场后,经
s返回电场;
(3)带电粒子开始运动后,第二次通过x轴时距O点的距离是0.6s?如果想使粒子返回到P点,在其它物理量不变的情况下,磁感应强度B应为1T.
| qE |
| m |
沿电场方向做匀加速直线运动,由y=
| 1 |
| 2 |
运动时间t1=
|
|
| 1 |
| 50 |
沿x轴方向的位移x=v0t1=0.2m
(2)粒子通过y轴进入磁场时在y方向上的速度vy=at1=10 m/s
因此,tanθ=
| vy |
| vx |
| 10 |
| 10 |
粒子在第二象限以O′为圆心做匀速圆周运动,圆弧所对的圆心角为α=270°,

运动时间t2=
| α |
| 360 |
| 3T |
| 4 |
T=
| 2πm |
| qB |
| 2×π |
| 0.5 |
| 1 |
| 50 |
| 2π |
| 25 |
②③联立得:t2=
| 3π |
| 50 |
(3)类平抛运动的水平位移:x1=v0t1=10×
| 1 |
| 50 |
匀速圆周运动洛伦兹力提供向心力,即qvB=m
| v2 |
| r |
v=
| 2 |
| 2 |
④⑤联立得:r=
2
| ||
| 5 |
由几何关系得匀速圆周运动的弦长:L=2rsin45°=
2
| ||
| 5 |
| ||
| 2 |
第二次通过x轴时距O点的距离是x2=L-x1=8-2m=6m
要让粒子再次回到P点,弦长L应为2x1
则粒子作圆周运动的半径R′=
| x1 |
| sin45° |
| 0.2 | ||||
|
| 2 |
由qvB=m
| v2 |
| r |
| mv |
| qR′ |
答;(1)带电粒子开始运动后,第一次通过x轴时距O点的距为0.2m;
(2)带电粒子进入磁场后,经
| 3π |
| 50 |
(3)带电粒子开始运动后,第二次通过x轴时距O点的距离是0.6s?如果想使粒子返回到P点,在其它物理量不变的情况下,磁感应强度B应为1T.
点评:本题是带电粒子在组合场中运动的问题,粒子垂直射入电场,在电场中偏转做类平抛运动,在磁场中做匀速圆周运动,要求同学们能画出粒子运动的轨迹,结合几何关系求解,知道半径公式及周期公式,难度较大.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图所示,在y>0的空间中存在着沿y轴正方的匀强电场;在y<0的空间中存在垂直xoy平面向里的匀强磁场.一个带负电的粒子(质量为m,电荷量为q,不计重力),从y轴上的P(0,b)点以平行于x轴的初速度υ0射入电场,经过x轴上的N(2b,0)点.求:
如图所示,在y>0的空间中存在着沿y轴正方的匀强电场;在y<0的空间中存在垂直xoy平面向里的匀强磁场.一个带负电的粒子(质量为m,电荷量为q,不计重力),从y轴上的P(0,b)点以平行于x轴的初速度υ0射入电场,经过x轴上的N(2b,0)点.求: 如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:
如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求: (2008?西城区一模)如图所示,在y>0的区域内有沿y轴正方向的匀强电场,在y<0的区域内有垂直坐标平面向里的匀强磁场.一电子(质量为m、电量为e)从y轴上A点以沿x轴正方向的初速度v0开始运动.当电子第一次穿越x轴时,恰好到达C点;当电子第二次穿越x轴时,恰好到达坐标原点;当电子第三次穿越x轴时,恰好到达D点.C、D两点均未在图中标出.已知A、C点到坐标原点的距离分别为d、2d.不计电子的重力.求:
(2008?西城区一模)如图所示,在y>0的区域内有沿y轴正方向的匀强电场,在y<0的区域内有垂直坐标平面向里的匀强磁场.一电子(质量为m、电量为e)从y轴上A点以沿x轴正方向的初速度v0开始运动.当电子第一次穿越x轴时,恰好到达C点;当电子第二次穿越x轴时,恰好到达坐标原点;当电子第三次穿越x轴时,恰好到达D点.C、D两点均未在图中标出.已知A、C点到坐标原点的距离分别为d、2d.不计电子的重力.求: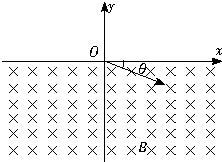 如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:该粒子射出磁场的位置(粒子所受重力不计)
如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:该粒子射出磁场的位置(粒子所受重力不计)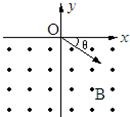 如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xoy平面并指向纸面外,磁感应强度为B.一带正电的粒子以速度v0从O点射入磁场,入射方向在xoy平面内,与x轴正向的夹角为θ.若粒子射出磁场的位置与O点的距离为l,求该粒子的电量和质量之比q/m及带点粒子在磁场中的运动时间.
如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xoy平面并指向纸面外,磁感应强度为B.一带正电的粒子以速度v0从O点射入磁场,入射方向在xoy平面内,与x轴正向的夹角为θ.若粒子射出磁场的位置与O点的距离为l,求该粒子的电量和质量之比q/m及带点粒子在磁场中的运动时间.