题目内容
如图所示，清洗楼房玻璃的工人常用一根绳索将自己悬在空中，工人及其装备的总重量为G，悬绳与竖直墙壁的夹角为a，悬绳对工人的拉力大小为F1，墙壁对工人的弹力大小为F2，则（ ）分析：工人受力平衡，合力为零，由平衡条件求出F1和F2．根据F1和F2的表达式分析讨论缓慢减小悬绳的长度时，F1与F2如何变化．
解答：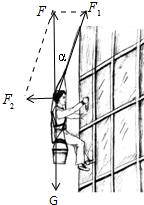
解：A、B分析工人受力：工人受到重力、支持力和拉力，如图
根据共点力平衡条件，有
水平方向：F1sinα=F2
竖直方向：F1cosα=G
解得，F1=
，F2=Gtanα．故AB错误．
C、D当缓慢减小悬绳的长度时，细绳与竖直方向的夹角α变大，故F1变大，F2变大，但F1与F2的合力与重力平衡，保持不变；故C错误，D正确．
故选D．
解：A、B分析工人受力：工人受到重力、支持力和拉力，如图根据共点力平衡条件，有
水平方向：F1sinα=F2
竖直方向：F1cosα=G
解得，F1=
| G |
| cosα |
C、D当缓慢减小悬绳的长度时，细绳与竖直方向的夹角α变大，故F1变大，F2变大，但F1与F2的合力与重力平衡，保持不变；故C错误，D正确．
故选D．
点评：本题关键是根据共点力平衡条件，由几何关系得到F1与F2的表达式，再讨论变化情况．
练习册系列答案
相关题目
（2012?湖南模拟）如图所示，清洗楼房玻璃的工人常用一根绳索将自己悬在空_中，工人及其装备的总重量为G，悬绳与竖直墙壁的夹角为a，悬绳对工人的拉力大小为F1，墙壁对工人的支持力大小为F2，则（ ）
如图所示，清洗楼房玻璃的工人常把一根绳索一端系于楼顶，另一端系在自己身上，将自己悬在空中，工人及其装备的总重量为G，悬绳与竖直墙壁的夹角为α，悬绳对工人的拉力大小为F1，墙壁对工人的弹力大小为F2，空中作业时工人与玻璃的水平距离为定值，则（ ）
如图所示，清洗楼房玻璃的工人常用一根绳索将自己悬在空中，工人及实装备的总重量为G，悬绳与竖直墙壁的夹角为a，悬绳对工人的拉力大小为F1 墙壁对工人的弹力大小为F2，则（ ）
如图所示，清洗楼房玻璃的工人常用一根绳索将自己悬在空中，工人及其装备的总重量为G，悬绳与竖直墙壁的夹角为α，悬绳对工人的拉力大小为F1，墙壁对工人的弹力大小为F2，则（ ）A、F1=
| ||
B、F2=
| ||
| C、若缓慢减小悬绳的长度，F1增大，F2增大 | ||
| D、若缓慢减小悬绳的长度，F1与F2的合力变大 |