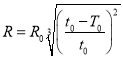��Ŀ����
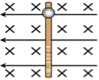
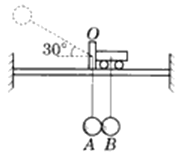
����Ŀ���ڹ⻬��ˮƽ����ͣ����һ������Ϊ�͵�С��������Ϊ����������һ�ᵯ�ɹ̶����������ɵ���һ����С����˹̶����ӣ�������ѹ������ϸ�߽���˨ס������ֹ��С���ϵģ��㣬��ͼ��ʾ�������M��Ķ�Ħ������Ϊ�̣��ϵ�Ϊ����ԭ��λ�ã���ϸ���նϺ����Ϳ�ʼ�˶���
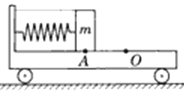
��1���������λ�ڣϵ������Ҳ࣬��������ٶ����Ҫ˵�����ɣ�
��2����������ﵽ����ٶȣ�1ʱ������������С���ƶ��˾�������ʱM���ٶȣ�2����һ�����е����ͷŵĵ������ܣ�����
��3���жϣ���͵������˶�״̬�Ǿ�ֹ�������˶�������������˶�������Ҫ˵�����ɣ�
���𰸡���1����O����ࣨ2�����ۣ��ͣ�������12��2�ͣ��̣��ݣ�3����������ն���ֹ
����������1�����ٶ�����λ��Ӧ��O����࣮��Ϊϸ���նϺ��ڵ��ɵ����ͻ���Ħ�����ĺ��������������������˶�����������Ħ�����ĺ���Ϊ��ʱ�������ٶȴﵽ���ʱ���ɱش���ѹ��״̬���˺�ϵͳ�Ļ�е�ܲ��ϼ�С�������ٴﵽ��һ����ٶȣ�
��2��ѡ������Ϊһϵͳ���ɶ����غ㶨�ɵã���1���ͣ�2��
����һ�����е����ͷŵĵ�������Ϊ��������
������![]() ����12��
����12��![]() �ͣ�22���̣����
�ͣ�22���̣����
���![]() ��
�� ![]() ��
��
��3����������ս���ֹ����Ϊϵͳ�����غ㣬���ܶ���Ϊ�㣬ֻҪ����ͼ�������˶�����Ҫ�˷�Ħ���������������������������ԣ���������ձض�����ֹ��

 ������������ϵ�д�
������������ϵ�д�