题目内容
12．
铝质薄平板的上方和下方分别有垂直于纸面的匀强磁场（图中未画出），一带电粒子从紧贴铝板上表面的A点沿图示方向射出，夹角θ=30°，从C点穿过铝板后到达铝板上的D点，粒子的运动轨迹如图所示．粒子从A运动到C的时间等于从C运动到D的时间．粒子穿越铝板时速度方向不变，粒子电荷量不变，重力不计．铝板上方和下方的磁感应强度大小之比为（ ）| A． | 0.2 | B． | $\frac{{\sqrt{2}}}{2}$ | C． | 1 | D． | 5 |
分析 由几何关系求得粒子在磁场中圆周运动转过的角度，根据周期求得粒子在磁场中运动的时间与周期的关系，根据时间相等求得周期关系，再由周期表达式求得磁感应强度之比即可．
解答 解：由题意由几何知道知，粒子在铝板上方运动的时间等于：
${t}_{1}=\frac{2θ}{360°}{T}_{1}$=$\frac{1}{6}{T}_{1}$
粒子在铝板下方圆周运动的时间等于
${t}_{2}=\frac{360°-2θ}{360°}{T}_{2}$=$\frac{5}{6}{T}_{2}$
由t1=t2
有：$\frac{{T}_{1}}{{T}_{2}}=\frac{5}{1}$
根据周期公式T=$\frac{2πm}{qB}$
可得$\frac{{T}_{1}}{{T}_{2}}=\frac{{B}_{2}}{{B}_{1}}=\frac{5}{1}$
即上方的磁感应强度是下方磁感应强度的$\frac{1}{5}$
故选：A．
点评 本题考查粒子在磁场中做圆周运动的时间表达式$t=\frac{θ}{2π}T$，根据洛伦兹力提供圆周运动向心力得出周期表达式是正确解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．
如图所示，劲度系数为k的轻质弹簧下端固定在倾角为θ的粗糙斜面底端的挡板C上，另一端自然伸长到A点．质量为m的物块从斜面上B点由静止开始滑下，与弹簧发生相互作用，最终停在斜面上某点．下列说法正确的是（ ）
如图所示，劲度系数为k的轻质弹簧下端固定在倾角为θ的粗糙斜面底端的挡板C上，另一端自然伸长到A点．质量为m的物块从斜面上B点由静止开始滑下，与弹簧发生相互作用，最终停在斜面上某点．下列说法正确的是（ ）| A． | 物块第一次滑到A点时速度最大 | |
| B． | 物块速度最大时弹簧的压缩量小于$\frac{mgsinθ}{k}$ | |
| C． | 物块压缩弹簧后被反弹过程做加速度逐渐减小的加速运动 | |
| D． | 物块最终停在斜面上时物块受到的摩擦力小于mgsinθ |
3．
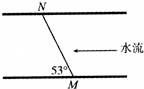2015年7月17日，一年一度的“中国Cg高校建德新安江龙舟赛”在建德新安江上展开角逐．如图某龙舟队在比赛前划向比赛点的途中要渡过48m宽两岸平直的河，河中水流的速度均为v=5.0m/s．龙舟从M处开出后沿直线MN实际航行到达对岸，若直线MN与河岸成53°角，龙舟在静水中的速度大小也为5.0m/s，已知sin53°=0.8，cos53°=0.6，则龙舟从M点沿直线MN到达对岸所经历的时间为（ ）
2015年7月17日，一年一度的“中国Cg高校建德新安江龙舟赛”在建德新安江上展开角逐．如图某龙舟队在比赛前划向比赛点的途中要渡过48m宽两岸平直的河，河中水流的速度均为v=5.0m/s．龙舟从M处开出后沿直线MN实际航行到达对岸，若直线MN与河岸成53°角，龙舟在静水中的速度大小也为5.0m/s，已知sin53°=0.8，cos53°=0.6，则龙舟从M点沿直线MN到达对岸所经历的时间为（ ）| A． | 4.8s | B． | 10s | C． | 14.4s | D． | 20s |
20．下列说法正确的是（ ）
| A． | 质点、位移都是理想化模型 | |
| B． | 牛顿的三个定律都可以通过实验来验证 | |
| C． | 单位m、kg、N是一组属于国际单位制的基本单位 | |
| D． | 伽利略指出力不是维持物体运动的原因 |
7．
如图，轻杆一端固定一小球，小球绕杆的另一端在竖直平面内做圆周运动，小球通过最高点时，（ ）
如图，轻杆一端固定一小球，小球绕杆的另一端在竖直平面内做圆周运动，小球通过最高点时，（ ）| A． | 杆对小球的作用力可能为零 | |
| B． | 如果杆对小球的作用力为推力，该推力不可能大于小球的重力 | |
| C． | 如果杆对小球的作用力为拉力，该拉力不可能大于小球的重力 | |
| D． | 如果杆对小球的作用力为推力，当小球通过最高点的速度减小时，该推力会增大 |
17．
如图，建筑工人用恒力F推运料车在水平地面上匀速前进，F与水平方向成30°角，运料车和材料所受重力之和为G，下列说法正确的是（ ）
如图，建筑工人用恒力F推运料车在水平地面上匀速前进，F与水平方向成30°角，运料车和材料所受重力之和为G，下列说法正确的是（ ）| A． | 建筑工人受地面摩擦力的方向水平向右 | |
| B． | 建筑工人受地面摩擦力的大小为$\frac{\sqrt{3}}{2}$G | |
| C． | 运料车受到地面的摩擦力的方向水平向右 | |
| D． | 运料车对地面压力为$\frac{F}{2}$+G |
1．（1）在“研究平抛运动”的实验中，采用图1的装置，已有下列器材：有孔的硬纸片、白纸、图钉、斜槽、刻度尺、钢球．还需要的器材有BCD．
A．秒表 B．平木板 C．重锤和细线 D．铅笔 E．天平 F．弹簧测力计
（2）在这个1装置中，把白纸固定在木板上的情况如图2所示，正确的是C．
（3）此实验中，斜槽末端保持水平的目的在于保证钢球做平抛运动，检测斜槽末端水平的方法是将钢球放置在槽口处轨道上，钢球能保持静止；钢球每次都要从斜槽上同一位置由静止释放，这样操作的目的是保证钢球每次做平抛运动的轨迹都重合．
（4）某同学在安装实验装置和进行其余的操作时都准确无误，他在分析数据时所建立的坐标系如图3所示，他的错误之处是直角坐标系的原点应建立在槽口末端正上方r（r为钢球半径）处，而该同学却错误地将坐标取在槽口处．
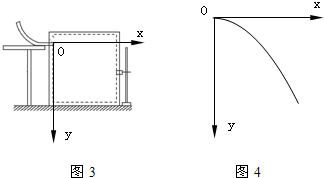
（5）此实验中，某同学按照正确的方法获得了运动的轨迹（如图4），建立了直角坐标系并测出了轨迹上四个点的坐标（如表）．
①根据这四个点的坐标，说明这条轨迹是抛物线的理由a是一个常量（设此轨迹方程：y=ax2．
则${a_1}=\frac{y_1}{x_1^2}=\frac{4.92}{{{{10.00}^2}}}=0.049$，
${a_2}=\frac{y_2}{x_2^2}=\frac{20.21}{{{{20.00}^2}}}=0.051$，
a3=$\frac{{y}_{3}}{{x}_{3}^{2}}$=$\frac{45.85}{3{0}^{2}}$=0.051，
a4=$\frac{{y}_{4}}{{x}_{4}^{2}}$=$\frac{81.65}{4{0}^{2}}$=0.051，
显然这四个值的相对误差不超过5%，这点误差在实验当中是允许的）；（要求具体过程）
②若这条轨迹是抛物线，求出平抛运动的初速度1.00m/s．（g=9.8m/s2）（保留三位有效数字）
A．秒表 B．平木板 C．重锤和细线 D．铅笔 E．天平 F．弹簧测力计
（2）在这个1装置中，把白纸固定在木板上的情况如图2所示，正确的是C．
（3）此实验中，斜槽末端保持水平的目的在于保证钢球做平抛运动，检测斜槽末端水平的方法是将钢球放置在槽口处轨道上，钢球能保持静止；钢球每次都要从斜槽上同一位置由静止释放，这样操作的目的是保证钢球每次做平抛运动的轨迹都重合．
（4）某同学在安装实验装置和进行其余的操作时都准确无误，他在分析数据时所建立的坐标系如图3所示，他的错误之处是直角坐标系的原点应建立在槽口末端正上方r（r为钢球半径）处，而该同学却错误地将坐标取在槽口处．
（5）此实验中，某同学按照正确的方法获得了运动的轨迹（如图4），建立了直角坐标系并测出了轨迹上四个点的坐标（如表）．
| x/cm | 10.00 | 20.00 | 30.00 | 40.00 |
| y/cm | 4.92 | 20.21 | 45.85 | 81.65 |
则${a_1}=\frac{y_1}{x_1^2}=\frac{4.92}{{{{10.00}^2}}}=0.049$，
${a_2}=\frac{y_2}{x_2^2}=\frac{20.21}{{{{20.00}^2}}}=0.051$，
a3=$\frac{{y}_{3}}{{x}_{3}^{2}}$=$\frac{45.85}{3{0}^{2}}$=0.051，
a4=$\frac{{y}_{4}}{{x}_{4}^{2}}$=$\frac{81.65}{4{0}^{2}}$=0.051，
显然这四个值的相对误差不超过5%，这点误差在实验当中是允许的）；（要求具体过程）
②若这条轨迹是抛物线，求出平抛运动的初速度1.00m/s．（g=9.8m/s2）（保留三位有效数字）
