题目内容
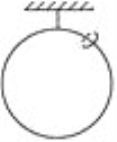
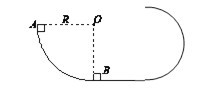
【题目】竖直平面内半径R=0.2m的四分之一光滑圆弧轨道下端与粗糙水平轨道相切,水平轨道长L=0.2m,右端与半径大于R的光滑圆弧轨道平滑相连,视为质点的小滑块A和B分别静止在圆弧轨道的最高点和最低点.现将A无初速释放,A与B碰撞后结合为一个整体,A和B的质量相等;A和B整体与桌面之间的动摩擦因数μ=0.2.物体始终没有离开轨道,重力加速度g取10m/s2.求:
(1)碰撞前瞬间A的速率v;
(2)碰撞后瞬间A和B整体的速率v′;
(3)A和B整体最终停止的位置离B距离.
【答案】(1)2m/s (2)1m/s(3)0.15m
【解析】
A到B的过程中,只有重力做功,机械能守恒,根据机械能守恒定律求出碰撞前A的速度;A、B碰撞的过程中动量守恒,根据动量守恒定律求出碰撞后整体的速率;对AB整体运用动能定理,求出AB整体在桌面上滑动的距离。
(1)根据机械能守恒定律有mgR=![]() mv2
mv2
解得碰撞前瞬间A的速率为:v=2 m/s.
(2)根据动量守恒定律有mv=2mv′
解得碰撞后瞬间A和B整体的速率:v′=![]() v=1 m/s.
v=1 m/s.
(3)根据动能定理有-μ·2m·gs=0-![]() ·2m·v′2
·2m·v′2
解得A和B整体沿水平桌面滑动的路程:![]()
位置离B距离:L=0.2-(0.25-0.2)m=0.15m

练习册系列答案
相关题目
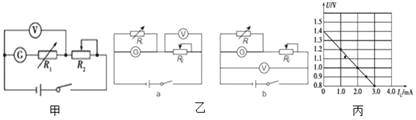
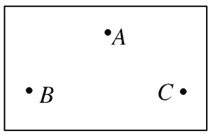
【题目】如图所示,已知黑箱外有A、B、C三只接线柱,黑箱内有一只定值电阻和一个二极管,它们的两端都直接接在接线柱上。多用电表依次测三只接线柱间的阻值,结果如表所示。请判定黑箱内的结构______。
红表笔 | A | A | B | C | C | B |
黑表笔 | B | C | C | B | A | A |
阻值(Ω) | 100 | 150 | 50 | 2 k | 2.1 k | 100 |