题目内容
A、B两个木块叠放在竖直轻弹簧上,如图所示,已知mA=mB=1kg,轻弹簧的劲度系数为100N/m.若在木块A上作用一个竖直向上的力F,使木块A由静止开始以2m/s2的加速度竖直向上做匀加速运动.取g=10m/s2.求:

(1)使木块A竖直向上做匀加速运动的过程中,力F的最大值是多少?
(2)若木块A竖直向上做匀加速运动,直到A、B分离的过程中,弹簧的弹性势能减小了1.28J,则在这个过程中,力F对木块做的功是多少?

(1)使木块A竖直向上做匀加速运动的过程中,力F的最大值是多少?
(2)若木块A竖直向上做匀加速运动,直到A、B分离的过程中,弹簧的弹性势能减小了1.28J,则在这个过程中,力F对木块做的功是多少?
(1)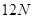 (2)
(2)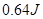
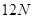 (2)
(2)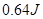
试题分析:(1)当F=0(即不加竖直向上F力时),设A、B叠放在弹簧上处于平衡时弹簧的压缩量为x,有
 解得:
解得:
当
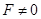 时,对B研究,受有重力、弹簧的弹力
时,对B研究,受有重力、弹簧的弹力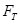 和A对B的压力
和A对B的压力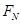 ,根据牛顿第二定律有
,根据牛顿第二定律有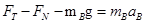
以木块A为研究对象进行受力分析,在重力、B对A的支持力和拉力作用下做匀加速运动,由牛顿第二定律得:
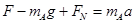
于是可知,当
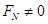 时,AB有共同加速度
时,AB有共同加速度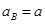 ,欲使木块A由静止开始以2m/s2的加速度竖直向上做匀加速运动,随
,欲使木块A由静止开始以2m/s2的加速度竖直向上做匀加速运动,随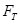 减小,
减小,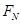 减小,
减小,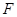 逐渐增大,当
逐渐增大,当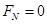 时,F有最大值,于是
时,F有最大值,于是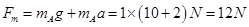
(2)由(1)知当
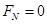 时,A、B开始分离,由
时,A、B开始分离,由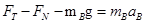 知,此时,弹簧压缩量为
知,此时,弹簧压缩量为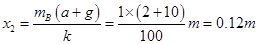
设A、B开始分离时共同速度为v,由运动学公式得:
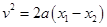 解得:
解得: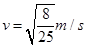
由题知,此过程弹性势能减少了
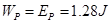
设F力功
 ,对这一过程应用动能定理得
,对这一过程应用动能定理得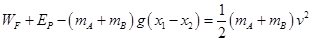
代入数据解得:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

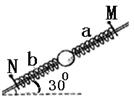
 ,连线与坐标轴+y方向的夹角为
,连线与坐标轴+y方向的夹角为 = 370,不计粒子的重力。(sin37o=0.6,cos37o=0.8)
= 370,不计粒子的重力。(sin37o=0.6,cos37o=0.8)
 中,粒子沿+y方向从O点射出,恰好经过A点;若在平行于y轴正方向的匀强电场
中,粒子沿+y方向从O点射出,恰好经过A点;若在平行于y轴正方向的匀强电场 中,粒子沿+x方向从O点射出,也恰好能经过A点,求这两种情况电场强度的比值
中,粒子沿+x方向从O点射出,也恰好能经过A点,求这两种情况电场强度的比值
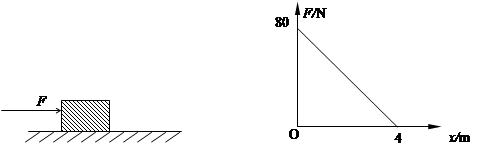
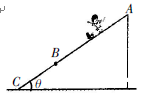
 ,BC段的动摩擦因数为
,BC段的动摩擦因数为 ,一个小朋友从A点开始下滑,滑到C点恰好静止,整个过程中滑梯保持静止状A态。则该小朋友从斜面顶端A点滑到底端 C点的过程中
,一个小朋友从A点开始下滑,滑到C点恰好静止,整个过程中滑梯保持静止状A态。则该小朋友从斜面顶端A点滑到底端 C点的过程中