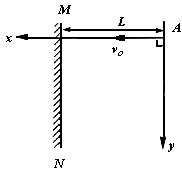
题目内容
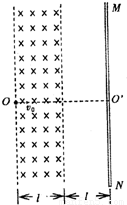
 如图所示,MN为一竖直放置足够大的荧光屏,距荧光屏左边l的空间存在着一宽度也为l、方向垂直纸面向里的匀强磁强.O′为荧光屏上的一点,OO′与荧光屏垂直,一质量为m、电荷量为q的带正电的粒子(重力不计)以初速度v0从O点沿OO′方向射入磁场区域.粒子离开磁场后打到荧光屏上时,速度方向与竖直方向成30°角.
如图所示,MN为一竖直放置足够大的荧光屏,距荧光屏左边l的空间存在着一宽度也为l、方向垂直纸面向里的匀强磁强.O′为荧光屏上的一点,OO′与荧光屏垂直,一质量为m、电荷量为q的带正电的粒子(重力不计)以初速度v0从O点沿OO′方向射入磁场区域.粒子离开磁场后打到荧光屏上时,速度方向与竖直方向成30°角.(1)求匀强磁场磁感应强度的大小和粒子打在荧光屏上时偏离O′点的距离;
(2)若开始时在磁场区域再加上与磁场方向相反的匀强电场(图中未画出),场强大小为E,则该粒子打在荧光屏上时的动能为多少?
分析:(1)带电粒子在磁场中做匀速圆周运动,由几何关系要求得带电粒子离开磁场时的速度方向,离开磁场后做匀速直线运动,由几何关系可求得偏离O′点的距离;
(2)加上电场后,带电粒子沿电场方向匀加速直线运动,由运动学公式可求得粒子在电场方向的速度;由动能定理可求得粒子打在屏上的动能.
(2)加上电场后,带电粒子沿电场方向匀加速直线运动,由运动学公式可求得粒子在电场方向的速度;由动能定理可求得粒子打在屏上的动能.
解答: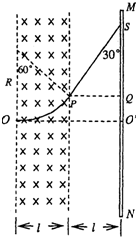 解:(1)粒子从O点射入,P点射出,沿直线运动到荧光
解:(1)粒子从O点射入,P点射出,沿直线运动到荧光
屏上的S点,如图所示,由几何关系可知,粒子在磁场中
作匀速圆周运动转过的圆心角θ=60° ①
运动轨道半径为:R=
②
而 qvB=m
③
由②、③解得:B=
④
根据几何关系可知:SQ=l?cot30° ⑤
O′Q=R-Rcos60° ⑥
由②、⑤、⑥解得O′S=O′Q+SQ=
⑦
(2)再加上电场后,根据运动的独立性,带电粒子沿电场方向匀加速运动,运动加速度
a=
⑧
粒子在磁场中运动时间为:t=
=
⑨
则粒子离开复合场时沿电场方向运动速度为 vE=at=
⑩
粒子打在荧光屏上时的动能为:Ek=
m
+
m
=
m
+
答:(1)匀强磁场磁感应强度的大小和粒子打在荧光屏上时偏离O′点的距离为
;
(2)该粒子打在荧光屏上时的动能为
m
+
.
 解:(1)粒子从O点射入,P点射出,沿直线运动到荧光
解:(1)粒子从O点射入,P点射出,沿直线运动到荧光屏上的S点,如图所示,由几何关系可知,粒子在磁场中
作匀速圆周运动转过的圆心角θ=60° ①
运动轨道半径为:R=
| l |
| sin60° |
而 qvB=m
| v2 |
| r |
由②、③解得:B=
| ||
| 2ql |
根据几何关系可知:SQ=l?cot30° ⑤
O′Q=R-Rcos60° ⑥
由②、⑤、⑥解得O′S=O′Q+SQ=
4
| ||
| 3 |
(2)再加上电场后,根据运动的独立性,带电粒子沿电场方向匀加速运动,运动加速度
a=
| qE |
| m |
粒子在磁场中运动时间为:t=
| πR |
| 3v0 |
2
| ||
| 9v0 |
则粒子离开复合场时沿电场方向运动速度为 vE=at=
2
| ||
| 9mv0 |
粒子打在荧光屏上时的动能为:Ek=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 E |
| 1 |
| 2 |
| v | 2 0 |
| 2(πlqE)2 | ||
27m
|
答:(1)匀强磁场磁感应强度的大小和粒子打在荧光屏上时偏离O′点的距离为
4
| ||
| 3 |
(2)该粒子打在荧光屏上时的动能为
| 1 |
| 2 |
| v | 2 0 |
| 2(πlqE)2 | ||
27m
|
点评:带电粒子在混合场中的运动要明确粒子运动的运动性质,根据运动性质寻找合适的解题方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目