Question

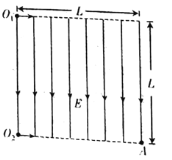
【题目】如图所示，一个方向竖直向下的有界匀强电场，电场强度大小为E。匀强电场左右宽度和上下宽度均为L。一个带正电荷的粒子(不计重力)从电场的左上方O1点以某一速度水平向右进入电场，该粒子刚好从电场的右下方A点离开电场；另一个质量为m、带电荷量为－q(q>0)的粒子(不计重力)从电场左下方O2点水平向右进入电场，进入电场时的初动能为Ek0。已知图中O1、O2、A在同一竖直面内，设O1点为坐标原点，水平向右为x轴正方向，竖直向下为y轴正方向，建立坐标系。

(1)求带正电荷的粒子的运动轨迹方程；

(2)求带负电荷的粒子运动到“带正电荷粒子的运动轨迹”处的动能；

(3)当带负电荷的粒子进入电场的初动能为多大时，它运动到“带正电荷粒子运动轨迹”处时的动能最小?动能的最小值为多少?

Answer 1

【答案】(1)；(2) ；(3)，

【解析】

考察电场中带电粒子运动的轨迹和能量变化。

取O1点为坐标原点，水平向右为x轴，竖直向下为y轴，建立平面直角坐标系，如图所示。

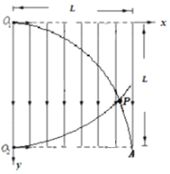
(1)对从O1点进入电场的粒子，设该粒子的加速度为a1，初速度为v1，设经过时间t，位置坐标为（x，y），有

水平方向

竖直方向

消去时间参数t得抛物线方程。

因为离开电场的A点坐标（L，L）在该抛物线上，所以坐标（L，L）满足抛物线方程，把坐标（L，L）代入抛物线方程得，代入抛物线方程可得其轨迹方程

(2)对从O2点进入电场的粒子，设质量为m、初速度为v0，加速度为a2，设经过时间t，位移坐标为（x，y），有：

水平方向

竖直方向

，

消去时间参数t得：

由题意有，联立求解得交点P（x,y)坐标为

，

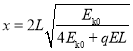从O2到P，对负粒子，根据动能定理有

解得。

(3) 变形为

由判别式=0

Ek=

解得Ek=（负值舍去），

二次函数开口向上，所以 ，即Ek的最小值为

时，电子进入电场的动能。

所以当带负电荷的粒子进入电场的动能为时，它运动到“带正电荷粒子运动轨迹”处时的动能最小，动能的最小值为。