题目内容
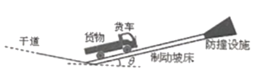
【题目】避险车道是避免恶性交通事故的重要设施，由制动坡床和防撞设施等组成，如图竖直平面内，制动坡床视为水平面夹角为θ（小角度）的斜面。一辆长L=12m的载有货物的货车因刹车失灵从干道驶入制动坡床，当车速为v1=23m/s时，车尾位于制动坡床的底端，货物开始在车厢内向车头滑动。当货物在车厢内滑动了s=4m时，车头距制动坡床顶端d=38m。再过一段时间，货车停止。已知空货车质量M是货物质量m的4倍，货物与车厢间的动摩擦因数μ=0.4；货车在制动坡床上运动受到的坡床阻力大小为货车和货物总重的0.44倍。货物与货车分别视为小滑块和平板，取cosθ=1，sinθ=0.1，g=10m/s2。
（1）请画出货物在车厢内滑动时受力示意图，并求货物在车厢内滑动时加速度的大小和方向；
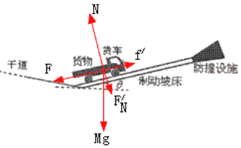
（2）请画出当货物在车厢内滑动时货车的受力示意图，并求出货车此时的的加速度的大小和方向；
（3）求出制动坡床的长度。
【答案】（1）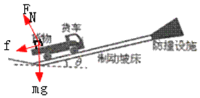
，5m/s2，方向沿制动坡床向下，
（2）
，5.5 m/s2，方向沿制动坡床向下，
（3）98m。
【解析】
（1）设货物的质量为m，货物在车厢内滑动时受到重力mg、支持力和沿车厢向下的摩擦力，如图所示：
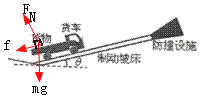
货物在车厢内滑动过程中，货物与车厢间的动摩擦因数μ=0.4，受摩擦力大小为f，加速度大小为a1，则：
f+mgsinθ=ma1
f=μmgcosθ
代入数据得：a1=5m/s2，方向沿制动坡床向下；
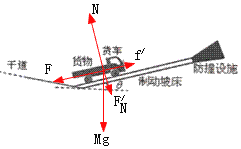
（2）设货车的质量为M，货车受到重力Mg、制动坡床对它的支持力N和阻力F、货物对它的压力
和摩擦力
，如图所示：
根据题意可得货车的质量为M=4m，设货车加速度为a2，货车受到制动坡床的阻力大小为F，F是货车和货物总重的k=0.44倍，则：
F=k(m+M)g
根据牛顿第二定律得：
Mgsinθ+F﹣f′=Ma2
其中：
f′=f=μmgcosθ
解得：a2=5.5m/s2，方向沿制动坡床向下；
（3）货车车尾位于制动坡床底端时的车速为v=23 m/s。货物在车厢内开始滑动到车头距制动坡床顶端d=38m的过程中，用时为t，货物相对制动坡床的运动距离为s2，货车长度L=12m，制动坡床的长度为x，则
货物运动位移为：
货车运动位移为：
且有：
由几何关系有：
x=L+d+s2
解得：x=98m。
