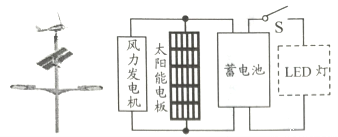
题目内容
【题目】如图所示,竖直放置的圆,其竖直直径为AB.小球在A点由静止释放,分别沿光滑轨道AC、AD、AE运动至圆周上C、D、E点,用时分别为t1、t2、t3,则( )
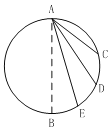
A. t1<t2<t3 B. t1>t2>t3 C. t1=t2=t3 D. t1<t2=t3
【答案】C
【解析】
先对任一轨道,分析小球的受力,再根据牛顿第二定律计算出小球沿任意一根轨道滑动的加速度,然后根据位移时间关系公式计算出时间,对表达式分析,得出时间与各因素的关系后得出结论。
对小球分析受力,小球受重力和支持力,将重力沿杆的方向和垂直杆的方向正交分解,根据牛顿第二定律得小球做初速度为零的匀加速直线运动,加速度为![]() ,(θ为杆与竖直方向的夹角)由图中的直角三角形可知,小球的位移 x=dcosθ(d是圆的直径)由x=
,(θ为杆与竖直方向的夹角)由图中的直角三角形可知,小球的位移 x=dcosθ(d是圆的直径)由x=![]() at2,解得:
at2,解得:![]() ,所以t与θ无关,即t1=t2=t3,故C正确,ABD错误。
,所以t与θ无关,即t1=t2=t3,故C正确,ABD错误。

练习册系列答案
相关题目