题目内容
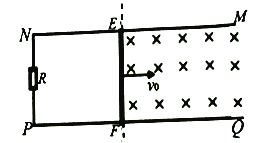
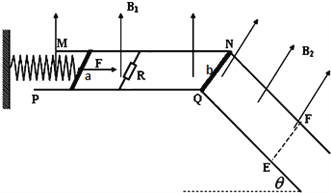
【题目】如图所示，光滑水平轨道MN、PQ和光滑倾斜轨道NF、QE在Q、N点连接，倾斜轨道倾角为
，轨道间距均为L．水平轨道间连接着阻值为R的电阻，质量分别为M、m，电阻分别为R、r的导体棒a、b分别放在两组轨道上，导体棒均与轨道垂直，a导体棒与水平放置的轻质弹簧通过绝缘装置连接，弹簧另一端固定在竖直墙壁上．水平轨道所在的空间区域存在竖直向上的匀强磁场，倾斜轨道空间区域存在垂直轨道平面向上的匀强磁场，该磁场区域仅分布在QN和EF所间的区域内，QN、EF距离为d，两个区域内的磁感应强度分别为
、
，以QN为分界线且互不影响．现在用一外力F将导体棒a向右拉至某一位置处，然后把导体棒b从紧靠分界线QN处由静止释放，导体棒b在出磁场边界EF前已达最大速度．当导体棒b在磁场中运动达稳定状态，撤去作用在a棒上的外力后发现a棒仍能静止一段时间，然后又来回运动并最终停下来．求：
（1）导体棒b在倾斜轨道上的最大速度
（2）撤去外力后，弹簧弹力的最大值
（3）如果两个区域内的磁感应强度
且导体棒电阻R=r，从b棒开始运动到a棒最终静止的整个过程中，电阻R上产生的热量为Q，求弹簧最初的弹性势能．
【答案】（1）
，（2）
，（3）
【解析】试题分析：（1）根据受力平衡条件，结合法拉第电磁感应定律与闭合电路欧姆定律，即可求解；（2）根据安培力与弹力平衡，结合安培力的表达式，即可求解；（3）根据能量守恒定律，结合焦耳定律，即可求解．
（1）b棒达到最大速度时，设b杆中的电流为I，则有： 
切割感应电动势为： 
由闭合电路欧姆定律得：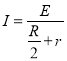 
联立解得： 
（2）撤去外力后，a杆将做减幅振动，最大弹力出现在其静止阶段
此时b杆正处于匀速运动阶段，则有： 
解得： 
（3）设b杆在磁场中运动期间，电阻R上产生的热量为
，a杆振动期间，电阻R上产生的热量为
,则有： 
因
，导体棒电阻R=r
在b杆在磁场中运动期间，由能量守恒定律： 
在a杆振动期间，由能量守恒定律： 
解得： 
