题目内容
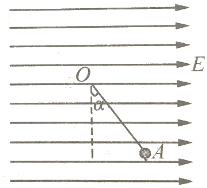
【题目】某柱形均匀透明玻璃构件的纵截面如图所示，左侧ABC区域为等腰直角三角形，AB长为L，右侧区域为半圆，BC为直径，下侧平行AB放置光屏MN，BC与MN垂直。现有一束宽度为L的平行光垂直AB边（不包括A、B两点）射向玻璃构件，通过玻璃构件后从右侧射出在光屏上形成光斑。已知该玻璃构件对该光的折射率为
，光在真空中的传播速度为c。（可能用到
，结果可用根式表示）求：
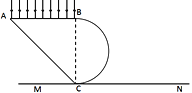
（1）光屏上所得光斑左侧与C点的距离；
（2）光在玻璃构件中最短的传播时间。
【答案】（1）
（2）
【解析】
做出光在透明玻璃构件中的光路图，在圆弧界面发生全反射的光线，射向光屏交MN的点，与C点最近，根据几何关系可求与C点的距离；由于光线在三角形内的路径长度相等，边界光线在玻璃中传播时间最短，根据几何关系可求最短距离，根据折射率求出光在玻璃中传播的速度，可求传播时间。
（i）画出某条光路图如图，光线在AC界面的入射角
由折射定律知
，可得临界角
光在AC界面发生全反射，水平射向圆弧界面
当在圆弧界面的入射角
时发生全反射，边界光线射向光屏交MN于P点，与C点最近
由三角形知识可知
（ii）由于光线在三角形内的路径长度相等，故边界光线在玻璃中传播时间最短，其路径总长度
光在玻璃中传播速度 
光在玻璃中传播最短时间
练习册系列答案
相关题目
