题目内容
如图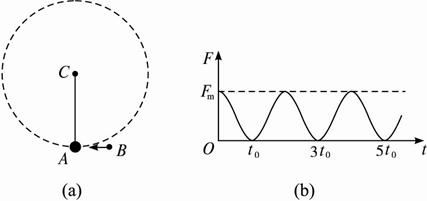
图
提示:子弹B沿水平方向以速度v0射入A内(未穿透),两者将获得一个共同速度v1,v1和v0的关系为m0v0=(m0+m1)v1,式中m是A的质量。?
解析:根据图象可以直接得到A、B共同做圆周运动的周期和在最高点和最低点的绳子的拉力,根据牛顿运动定律可以列出方程。又因为A、B共同运动时遵循机械能守恒定律,根据机械能守恒定律可以找出最高点和最低点的速度关系。?
解:由图(b)可直接看出,A、B一起做周期性运动,运动的周期T=2t0? ①
令m表示A的质量,l表示绳长,v 1表示B陷入A内时即t=0时A、B的速度(即圆周运动最低点的速度),v2表示运动到最高点时的速度,F1表示运动到最低点时绳的拉力,F2表示运动到最高点时绳的拉力,根据动量守恒定律,得?
m0v0=(m0+m)v1 ②
在最低点和最高点处运用牛顿定律可得?
F1-(m+m0)g=(m+m0) ![]() ③
③
F2+(m+m0)g=(m+m0) ![]() ④
④
根据机械能守恒定律可得?
![]() (m+m0)v12-
(m+m0)v12-![]() (m+m0)v22 ⑤
(m+m0)v22 ⑤
由图(b)可知F2=0 ⑥
F1=Fm ⑦
由以上各式可解得,反映系统性质的物理量是m=![]() -m0 ⑧
-m0 ⑧
l=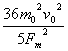 ⑨
⑨
A、B一起运动过程中的守恒量是机械能E,若以最低点为势能的零点,则?
E=![]() (m+m0)v12 ⑩
(m+m0)v12 ⑩
由②⑧⑩式解得 E=![]() g。
g。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
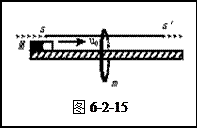 A.磁铁穿过金属环后,二者将先后停下来
A.磁铁穿过金属环后,二者将先后停下来