题目内容
如图所示,一个由轻杆组成的等边三角形ABO的A点和B点分别固定着质量为m和2m的小球,三角形ABO可绕光滑的水平转轴O自由转动,现使OA处于竖直位置,OB与水平方向的夹角为300,此时将它们由静止释放,不考虑空气阻力作用,则( )
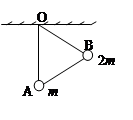

| A.B球到达最低点时速度为零 |
| B.A球向左摆动所能达到的最高点应高于B球开始运动时的最高点 |
| C.当它们从左向右回摆时,B球一定能回到起始位置 |
| D.B球到达最低点的过程中,B球机械能的减少量等于A球机械能的增加量 |
BCD
试题分析:在摆动过程中,2m减少势能多于m增加势能,所以2m运动到最低点速度不为零,即m在2m等高处速度不为零,A错。由于m在2m等高处速度不为零,所以A球向左摆动所能达到的最高点应高于B球开始运动时的最高点,B对。由于整个装置不考虑摩擦,所以机械能守恒,即当它们从左向右回摆时,B球一定能回到起始位置,C对。在整个过程中B减少机械能,等于A机械能增加量,整体机械能才会守恒,D对
点评:本题考查了整体的机械能守恒定律,B、A的机械能不守恒,但是由于整体没有出现其他能量,只有势能以及动能相互转化,所以整体机械能守恒。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
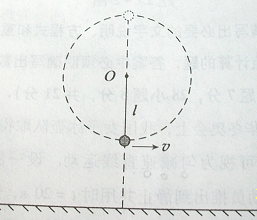
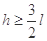
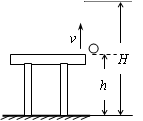
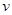 竖直向上抛出,桌面离地高度为h,小球能达到的最大离地高度为H。若以桌面作为参考平面,不计空气阻力,则( )
竖直向上抛出,桌面离地高度为h,小球能达到的最大离地高度为H。若以桌面作为参考平面,不计空气阻力,则( )